江苏省泰州市姜堰区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-27 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，是中心对称图形，但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查中，适合用普查方式的是(　　)

A、对夏季冷饮市场上冰淇淋质量的调査 B、对全市中学生的视力情况进行调查 C、对航天飞机零部件的调査 D、对一批节能冰箱使用寿命的调査

查看试题解析
3. 下列事件中，不可能事件是(　　)

A、打开电视，正在播放广告 B、小明家买一张彩票获得500万大奖 C、太阳从西方升起 D、三天内将下雨

查看试题解析
4. 如果关于x的分式方程 $\frac{m}{x - 2} + \frac{2 x}{x - 2} = 1$ 有增根，那么m的值为(　　)

A、﹣2 B、2 C、4 D、﹣4

查看试题解析
5. 某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p(Pa)是气球体积V(m³)的反比例函数，且当V=1.5m³时，p=16000Pa，当气球内的气压大于40000Pa时，气球将爆炸，为确保气球不爆炸，气球的体积应(　　)

A、不小于0.5m³ B、不大于0.5m³ C、不小于0.6m³ D、不大于0.6m³

查看试题解析
6. 在▱ABCD中，∠ABC的角平分线交线段AD于点E，DE=1，点F是BE中点，连接CF，过点F作FG⊥BC，垂足为G，设AB=x，若▱ABCD的面积为8，FG的长为整数，则整数x的值为(　　)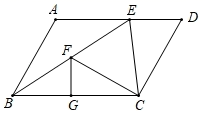

A、1 B、2 C、3 D、2或3

查看试题解析

二、填空题

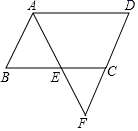
7. 据媒体报道，某市因环境污染造成的经济损失每年高达3400000元，数据3400000用科学记数法表示为.

查看试题解析
8. 在单词“BANANA”中随机选择一个字母，选到字母“N”的概率是.

查看试题解析
9. 如果二次根式 $\sqrt{3 - x}$ 有意义，那么 $x$ 的取值范围是.

查看试题解析
10. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值等于．

查看试题解析
11. 双曲线y $= \frac{3 + 2 m}{x}$ 在每一象限内y随x的增大而减小，则m的取值范围是.

查看试题解析
12. 已知m是 $\sqrt{5}$ 的小数部分，则 $\frac{1}{m + 2} =$ .

查看试题解析
13. 如图，在▱ABCD中，E是边BC上一点，且AB=BE，AE、DC的延长线相交于点F，∠F=62°，则∠D=°.

查看试题解析
14. 若x＜2，化简 $\sqrt{{(x - 2)}^{2}} - | 4 - x |$ 的结果是.

查看试题解析
15. 如图，点A、B是反比例函数y $= \frac{k}{x}$ (x＜0)图象上的两点，过点A、B分别作AC⊥x轴于点C，BD⊥x轴于点D，连接OA、BC，已知点C(﹣1，0)，BD=2， $S_{△ B C D} = \frac{1}{2} S_{△ A O C}$ ，则k=.

查看试题解析
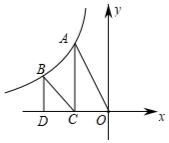16. 在Rt△ABC中，∠C=90°，AC=3，BC=4，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN、MN的中点，则DE长度的取值范围是.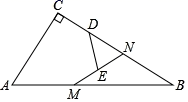

查看试题解析

三、解答题

17. 计算：

(1)、|1 $- \sqrt{2}$ |+( $\frac{1}{2}$ )^﹣¹ $+ \sqrt{8}$

(2)、 $(2 \sqrt{3} - \sqrt{6}) \times \sqrt{3}$

查看试题解析
18. 解方程 $\frac{x}{x - 1} - 1 = \frac{3}{x^{2} - 1}$ .

查看试题解析
19. 先化简，再求值： $\frac{a - b}{2 a} \div$ (a $- \frac{2 a b - b^{2}}{a}$ )，其中a﹣b=2.

查看试题解析
20. 某中学计划根据学生的兴趣爱好组建课外兴趣小组，并随机抽取了部分同学的兴趣爱好进行调查，将收集的数据整理并绘制成下列两幅统计图，请根据图中的信息，完成下列问题：

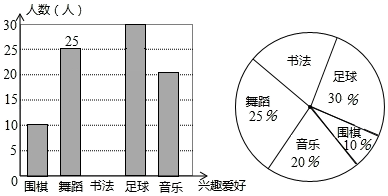(1)、学校这次调查共抽取了名学生；

(2)、求抽取的学生中喜欢书法的人数，并补全条形统计图；

(3)、在扇形统计图中，“围棋”所在扇形的圆心角度数为度；

(4)、设该校共有学生2000名，请你估计该校有多少名学生喜欢足球.

查看试题解析
21. 为了改善生态环境，防止水土流失，某村计划在荒坡上种树480棵，由于青年志愿者支援，实际每天种树的棵数是原计划的1.5倍，结果提前4天完成任务，原计划每天种树多少棵？

查看试题解析
22. 如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(﹣2，2)，B(0，5)，C(0，2).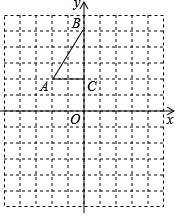

（ 1 ）将△ABC以点C为旋转中心顺时针旋转90°，得到△A₁B₁C，请画出△A₁B₁C的图形.

（ 2 ）平移△A₁B₁C，使点A₁的对应点A₂坐标为(2，0)，请画出平移后对应的△A₂B₂C₂的图形.

（ 3 ）若将△ABC绕某一点旋转可得到△A₂B₂C₂ ，请直接写出旋转中心的坐标.

查看试题解析
23. 如图，一次函数y=x+6的图象与反比例函数y $= \frac{k}{x}$ (x＜0)的图象交于A(﹣1，a)、B(b，1)两点.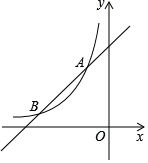

(1)、求a、b、k的值；

(2)、当一次函数的值大于反比例函数的值时，根据图象写出自变量x的取值范围；

(3)、求△ABO的面积.

查看试题解析
24. 如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连接BP、EQ.

(1)、求证：四边形BPEQ是菱形；

(2)、若AB=6，BE=10，求PQ的长.

查看试题解析
25. 点C为线段AB上一点，分别以AC、BC为边在线段AB的同侧作正方形ACDE和BCFG，连接AF、BD.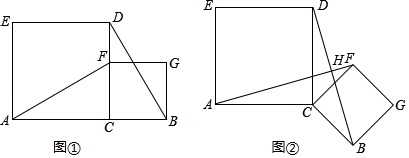

(1)、如图①，AF与BD的数量关系和位置关系分别为；

(2)、将正方形BCFG绕着点C顺时针旋转α角(0°＜α＜360°)，
①如图②，第（1）问的结论是否仍然成立？请说明理由.

②若AC=4，BC=2 $\sqrt{2}$ ，当正方形BCFG绕着点C顺时针旋转到点A、B、F三点共线时，求DB的长度.

查看试题解析
26. 如图所示，一次函数y=kx+b的图象与反比例函数y $= \frac{m}{x}$ 交于A(1，t+2)，B(﹣2t，﹣1)两点.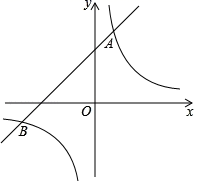

(1)、求一次函数和反比例函数的函数表达式；

(2)、点C(x₁ ， y₁)和D(x₂ ， y₂)是反比例函数y $= \frac{m}{x}$ 图象上任意两点，
①若x₁＜x₂＜0，p $= \frac{y_{1} + y_{2}}{8}$ ，q $= \frac{2}{x_{1} + x_{2}}$ ，试判断p、q的大小关系，并说明理由；

②若x₁＜﹣4，0＜x₂＜1，过C、D两点分别作直线AB的垂线，垂足分别为E、F，当x₁x₂=﹣4时，判断四边形CEFD的形状，并说明理由.

查看试题解析