江苏省南京市秦淮区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
1. 下列交通标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,不适合用普查的是( )A、了解全班同学每周体育锻炼的时长 B、“新冠”肺炎疫情期间检测地铁乘客的体温 C、某学校招艺术特长生,对报名学生进行面试 D、了解全国中学生每天写作业的时长3. 下列运算中,正确的是( )A、 B、 C、 D、4. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、打开电视,正在播放广告 C、抛掷一枚质地均匀且6个面上分别标上数字1~6的骰子,朝上一面的数字小于7 D、一个不透明的袋子中只装有2个黑球,搅匀后从中随机摸出一个球,结果是红球5. 下列分式变形中,正确的是( )A、 B、 C、 D、6. 如图,A(a,b)、B(-a,-b)是反比例函数 的图象上的两点.分别过点A、B作y轴的平行线,与反比例函数 的图象交于点C、D.若四边形ACBD的面积是4,则m、n满足等式( )
2. 下列调查中,不适合用普查的是( )A、了解全班同学每周体育锻炼的时长 B、“新冠”肺炎疫情期间检测地铁乘客的体温 C、某学校招艺术特长生,对报名学生进行面试 D、了解全国中学生每天写作业的时长3. 下列运算中,正确的是( )A、 B、 C、 D、4. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、打开电视,正在播放广告 C、抛掷一枚质地均匀且6个面上分别标上数字1~6的骰子,朝上一面的数字小于7 D、一个不透明的袋子中只装有2个黑球,搅匀后从中随机摸出一个球,结果是红球5. 下列分式变形中,正确的是( )A、 B、 C、 D、6. 如图,A(a,b)、B(-a,-b)是反比例函数 的图象上的两点.分别过点A、B作y轴的平行线,与反比例函数 的图象交于点C、D.若四边形ACBD的面积是4,则m、n满足等式( )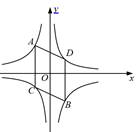 A、m+n=4 B、n-m=4 C、m+n=2 D、n-m=2
A、m+n=4 B、n-m=4 C、m+n=2 D、n-m=2二、填空题
-
7. 若代数式 在实数范围内有意义,则x的取值范围是。8. 化简 的结果是.9. 转动如图的转盘(转盘中各个扇形的面积都相等),当它停止转动时,指针指向标有数字的区域的可能性最小.
 10. 在矩形ABCD中,AC与BD相交于点O,若OA=2,则BD的长是.11. 已知反比例函数y= 的图象位于第一、第三象限,则k的取值范围是.12. 比较大小: (填“>”或“<”=).13. 小丽抽样调查了学校40名同学的体重(均精确到1 kg),绘制了如下频数分布直方图,那么在该样本中体重不小于55 kg的频率是.
10. 在矩形ABCD中,AC与BD相交于点O,若OA=2,则BD的长是.11. 已知反比例函数y= 的图象位于第一、第三象限,则k的取值范围是.12. 比较大小: (填“>”或“<”=).13. 小丽抽样调查了学校40名同学的体重(均精确到1 kg),绘制了如下频数分布直方图,那么在该样本中体重不小于55 kg的频率是.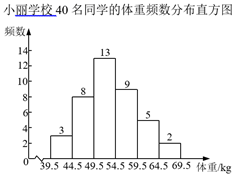 14. 如图,两个正方形Ⅰ,Ⅱ和两个矩形Ⅲ,Ⅳ拼成一个大正方形,已知正方形Ⅰ,Ⅱ的面积分别为10和3,那么大正方形的面积是.
14. 如图,两个正方形Ⅰ,Ⅱ和两个矩形Ⅲ,Ⅳ拼成一个大正方形,已知正方形Ⅰ,Ⅱ的面积分别为10和3,那么大正方形的面积是.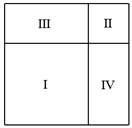 15. 如图,已知∠AOB=45°,将射线OA绕点O逆时针旋转α°(0 α 360),得到射线OA′.若OA′⊥OB,则α的值是.
15. 如图,已知∠AOB=45°,将射线OA绕点O逆时针旋转α°(0 α 360),得到射线OA′.若OA′⊥OB,则α的值是. 16. 如图,在△ABC中,∠BAC=90°,AB=AC,P是△ABC内一点.若PA=1,PC=2,∠APC=135°,则PB的长为.
16. 如图,在△ABC中,∠BAC=90°,AB=AC,P是△ABC内一点.若PA=1,PC=2,∠APC=135°,则PB的长为.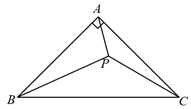
三、解答题
-
17. 解方程:(1)、(2)、18. 计算:(1)、(2)、19. 先化简,再求值: ,其中x=-1.20. 为了了解某小区今年6月份家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计表和统计图:

根据以上信息,解答下列问题:
(1)、本次抽样调查的样本容量是 , m的值为 , n的值为;(2)、若该小区共有500户家庭,请估计该月有多少户家庭用水量不超过9.0吨?21. 在压力不变的情况下,某物体所受到的压强p(Pa)与它的受力面积S(m2)之间成反比例函数关系,其图象如图所示.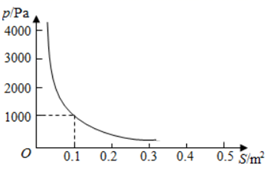 (1)、求p与S之间的函数表达式;(2)、当S=0.4 m2时,求该物体所受到的压强p.22. 如图,四边形ABCD是菱形,E、F、G、H分别是边AB、BC、CD、DA的中点,连接EF、FG、GH、HE.求证:四边形EFGH是矩形.
(1)、求p与S之间的函数表达式;(2)、当S=0.4 m2时,求该物体所受到的压强p.22. 如图,四边形ABCD是菱形,E、F、G、H分别是边AB、BC、CD、DA的中点,连接EF、FG、GH、HE.求证:四边形EFGH是矩形.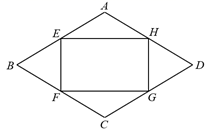 23. 甲、乙两公司为“见义勇为基金会”各捐款30 000元.已知乙公司比甲公司人均多捐20元,且甲公司的人数比乙公司的人数多20%,设乙公司有x人.(1)、用含x的代数式填表(结果不需要化简):
23. 甲、乙两公司为“见义勇为基金会”各捐款30 000元.已知乙公司比甲公司人均多捐20元,且甲公司的人数比乙公司的人数多20%,设乙公司有x人.(1)、用含x的代数式填表(结果不需要化简):人均捐款额(元/人)
人数
捐款总额(元)
甲公司
30000
乙公司
x
30000
(2)、求x的值.24. 题目: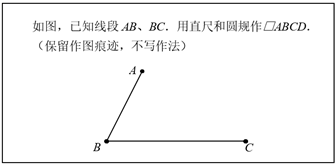 (1)、下图是小明所作的图,根据作图痕迹,可以知道他作图的依据是“的四边形是平行四边形”;
(1)、下图是小明所作的图,根据作图痕迹,可以知道他作图的依据是“的四边形是平行四边形”;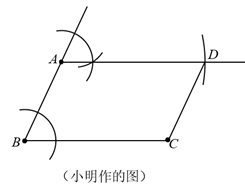 (2)、请你以“对角线互相平分的四边形是平行四边形”为依据完成题目中的作图.25.(1)、分式 有意义的条件是 , 该分式的值(填“会”或“不会”)为零,由此可以判断出反比例函数 的图象与y轴和x轴都没有公共点.(2)、类比(1),下列直线中,与函数 的图象没有公共点的是.(填写所有满足要求的选项的序号)
(2)、请你以“对角线互相平分的四边形是平行四边形”为依据完成题目中的作图.25.(1)、分式 有意义的条件是 , 该分式的值(填“会”或“不会”)为零,由此可以判断出反比例函数 的图象与y轴和x轴都没有公共点.(2)、类比(1),下列直线中,与函数 的图象没有公共点的是.(填写所有满足要求的选项的序号)①经过点(1,0)且平行于y轴的直线;
②经过点(-1,0)且平行于y轴的直线;
③经过点(0,2)且平行于x轴的直线;
④经过点(0,-2)且平行于x轴的直线.
(3)、已知函数 的图象可以由 的图象平移得到.请你结合(2)中的结论,画出函数 的图象,并写出该函数的两条不同类型的性质.26. 我们知道,平行四边形的对边平行且相等.利用这一性质,可以为证明线段之间的位置关系和数量关系提供帮助.(1)、重温定理,识别图形如图①,我们在探究三角形中位线DE和第三边BC的关系时,所作的辅助线为“延长DE到点F,使EF=DE,连接CF”,此时DE与DF在同一直线上且DE= DF,又可证图中的四边形为平行四边形,可得BC与DF的关系是 , 于是推导出了“DE BC,DE= BC”.
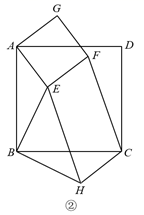
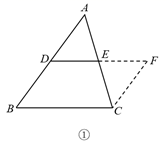 (2)、寻找图形,完成证明
(2)、寻找图形,完成证明如图②,四边形ABCD和四边形AEFG都是正方形,△BEH是等腰直角三角形,∠EBH=90°,连接CF、CH.求证CF= BE.
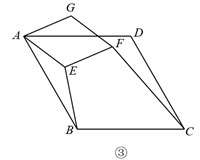
 (3)、构造图形,解决问题
(3)、构造图形,解决问题如图③,四边形ABCD和四边形AEFG都是菱形,∠ABC=∠AEF=120°,连接BE、CF.直接写出CF与BE的数量关系.