山东省滕州市2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. $- \sqrt{3}$ 的倒数是（）．

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $- \sqrt{3}$ D、 $\frac{- \sqrt{3}}{3}$

查看试题解析
2. 若 $\sqrt{a^{2}} = - a$ ，则a的取值范围是（）

A、全体实数 B、 $a = 0$ C、 $a \geq 0$ D、 $a \leq 0$

查看试题解析
3. 下列变形正确的是（）

A、 $\sqrt{(- 16) (- 25)} = \sqrt{- 16} \times \sqrt{- 25}$ B、 $\sqrt{16 \frac{1}{4}} = \sqrt{16} \times \sqrt{\frac{1}{4}} = 4 \times \frac{1}{2} = 2$ C、 $\sqrt{{(a + b)}^{2}}$ ＝|a+b| D、 $\sqrt{25^{2} - 24^{2}}$ ＝25﹣24＝1

查看试题解析
4. 给出下列结论：① $\sqrt{10} + 1$ 在3和4之间；② $\sqrt{x + 1}$ 中 $x$ 的取值范围是 $x \geq - 1$ ；③ $\sqrt{81}$ 的平方根是3；④ $- \sqrt[3]{- 125} = - 5$ ；⑤ $\frac{\sqrt{5} - 1}{2} > \frac{5}{8}$ ．其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如果 $a < 0 ， b < 0$ ，且 $a - b = 6$ ，则 $\sqrt{a^{2}} - \sqrt{b^{2}}$ 的值是（）

A、6 B、-6 C、6或-6 D、无法确定

查看试题解析
6. 已知点P₁(a﹣1，5)和P₂(2，b﹣1)关于x轴对称，则(a+b)²⁰¹⁹的值为（）

A、 ${(- 3)}^{2019}$ B、 $3^{2019}$ C、1 D、﹣1

查看试题解析
7. 长度分别为9cm、12 cm、15 cm、36 cm、39 cm五根木棍首尾连接，最多可搭成直角三角形的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图 $R t △ A B C$ ， $∠ C = 90 °$ ，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”；当 $A C = 1$ ， $B C = 2 \sqrt{2}$ ，计算阴影部分的面积为（）

A、 $\sqrt{2}$ B、 $\sqrt{2} π$ C、 $2 \sqrt{2} π$ D、 $2 \sqrt{2}$

查看试题解析
9. 在直角坐标系中， $O$ 为坐标原点，已知点 $A (1 ， 2)$ ，在坐标轴上确定点 $P$ ，使得 $△ A O P$ 为直角三角形，则符合条件的点 $P$ 的个数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 已知点P（m ， n）在第四象限，则直线y=nx+m图象大致是下列的（　　）.

A、 B、 C、 D、

查看试题解析
11. 点 $P_{1} (x_{1} ， y_{1})$ ，点 $P_{2} (x_{2} ， y_{2})$ 是一次函数 $y = - 4 x + 3$ 图象上的两个点，且 $x_{1} < x_{2} < 0$ ，则3， $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{2} < y_{1} < 3$ B、 $y_{1} > y_{2} > 3$ C、 $y_{1} < y_{2} = 3$ D、 $y_{1} = y_{2} > 3$

查看试题解析
12. 对于任意的正数m，n定义运算※为：m※n＝ ${\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ 计算(3※2)×(8※12)的结果为（）

A、2－4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析
13. 我们知道：四边形具有不稳定性.如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（）

A、（ $\sqrt{3}$ ，1） B、（2，1） C、（2， $\sqrt{3}$ ） D、（1， $\sqrt{3}$ ）

查看试题解析
14. 如图是某蓄水池的横断面示意图，分为深水池和浅水池，如果向这个蓄水池以固定的流量注水，下面能大致表示水的最大深度 $h$ 与时间 $t$ 之间的关系的图象是（）

A、 B、 C、 D、

查看试题解析
15. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟．在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：①甲步行的速度为60米/分；②乙走完全程用了30分钟；③乙用16分钟追上甲；④乙到达终点时，甲离终点还有320米其中正确的结论有（）

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析

二、填空题

16. 已知一个正数的两个平方根分别为2m﹣6和3+m ，则m﹣9的立方根是．

查看试题解析
17. 如图，直线l上有三个正方形a，b，c，若a，c的面积分别为7和9，则b的面积为.

查看试题解析
18. 将直线y＝﹣2x+1向上平移2个单位长度，所得到的直线解析式.

查看试题解析
19. 已知点P的坐标为（2-a，3a+6），且点P到两坐标轴的距离相等，则a= ．

查看试题解析
20. 如图，直线y=2x+4与x，y轴分别交于A，B两点，以OB为边在y轴右侧作等边三角形OBC，将点C向左平移，使其对应点C′恰好落在直线AB上，则点C′的坐标为．

查看试题解析
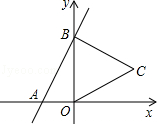21. 如图1，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水， $28 s$ 时注满水槽，水槽内水面的高度 $y (c m)$ 与注水时间 $x (s)$ 之间的函数图象如图2所示.如果将正方体铁块取出，又经过秒恰好将水槽注满.

查看试题解析

三、解答题

22. 计算题：

(1)、 $\frac{\sqrt{12} + \sqrt{27}}{\sqrt{3}} - {(\sqrt{3} - \sqrt{2})}^{2} - | - \sqrt{6} |$

(2)、 $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$ ．

查看试题解析
23. 如图，△ABC中，D是BC上的一点．若AB＝10，BD＝6，AD＝8，AC＝17，求△ABC的面积．

查看试题解析
24. 在平面直角坐标系中，已知△ABC顶点坐标分别为A(0，3)，B(1，1)，C(﹣3，﹣1)，△DEF与△ABC关于y轴对称，且A，B，C依次对应D，E，F，

(1)、请写出D，E，F的坐标.

(2)、在平面直角坐标系中画出△ABC和△DEF.

(3)、经过计算△DEF各边长度，发现DE、EF、FD满足什么关系式，写出关系式.

(4)、求△DEF的面积.

查看试题解析
25. 阅读下列解题过程：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) \times (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{{(\sqrt{2})}^{2} - 1^{2}} = \sqrt{2} - 1$

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \frac{\sqrt{3} - \sqrt{2}}{{(\sqrt{3})}^{2} - {(\sqrt{2})}^{2}} = \sqrt{3} - \sqrt{2}$

请回答下列问题：

(1)、归纳：观察上面的解题过程，请直接写出下列各式的结果．① $\frac{1}{\sqrt{7} + \sqrt{6}} =$ ；② $\frac{1}{\sqrt{n} + \sqrt{n - 1}} =$ ．

(2)、应用：求 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \frac{1}{\sqrt{5} + \sqrt{4}} + \dots + \frac{1}{\sqrt{10} + \sqrt{9}}$ 的值；

(3)、拓展： $\frac{1}{\sqrt{3} - 1} - \frac{1}{\sqrt{5} - \sqrt{3}} + \frac{1}{\sqrt{7} - \sqrt{5}} - \frac{1}{\sqrt{9} - \sqrt{7}} =$ ．（直接写出答案）

查看试题解析
26. 如图，在长方形 $O A B C$ 中， $O$ 为平面直角坐标系的原点，点 $A$ 坐标为 $(a ， 0)$ ，点 $C$ 的坐标为 $(0 ， b)$ ，且 $a$ ， $b$ 满足 $\sqrt{a - 4} + | b - 6 | = 0$ ，点 $B$ 在第一象限内，点 $P$ 从原点出发，以每秒2个单位长度的速度沿着 $O - C - B - A - O$ 的线路移动．

(1)、点 $B$ 的坐标为；

(2)、当点 $P$ 移动4秒时，请指出点 $P$ 的位置，并求出点 $P$ 的坐标；

(3)、在移动过程中，当点 $P$ 到 $x$ 轴的距离为5个单位长度时，求点 $P$ 移动的时间．

查看试题解析
27. 一农民带了土豆进城出售，为了方便，他带了一些零用钱备用，按市场价出售一些土豆后，又降价出售，售出土豆的千克数 $x$ 与他手中持有的钱数 $y$ （含零用钱）的关系如图．结合图象回答：

(1)、农民自带的零钱是多少元？

(2)、求出降价前 $y$ 与 $x$ 之间的函数关系式；

(3)、降价后他按每千克1.6元将土豆售完，这时他手中的钱（含零用钱）是86元，那么他一共带了多少土豆去城里出售？

查看试题解析
28. 如图，直线 $y = k x - 1$ 与 $x$ 轴， $y$ 轴分别交于 $B$ ， $C$ 两点，且 $O B = \frac{1}{2} O C$ ．

(1)、求 $B$ 点的坐标和 $k$ 的值；

(2)、若点 $A (x ， y)$ 是直线 $y = k x - 1$ 第一象限部分上的一个动点，试写出 $△ A O B$ 的面积与 $x$ 的函数关系式；

(3)、点 $D$ 在直线 $y = k x - 1$ 运动，当点 $D$ 运动到什么位置时， $△ D O B$ 的面积是 $\frac{1}{4}$ ？求出此时 $D$ 点坐标．

查看试题解析