山东省青岛市李沧区2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列三角形是直角三角形的是( )A、
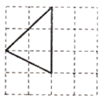 B、
B、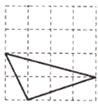 C、
C、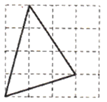 D、
D、 3. 的立方根是( )A、2 B、4 C、±2 D、±84. 若点P(m+3,m-2)在直角坐标系的x轴上,则点P的坐标为( )A、(0,5) B、(5,0) C、(-5,0) D、(0,-5)5. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间6. 在某次试验中,测得两个变量 和 之间的4组对应数据如下表:
3. 的立方根是( )A、2 B、4 C、±2 D、±84. 若点P(m+3,m-2)在直角坐标系的x轴上,则点P的坐标为( )A、(0,5) B、(5,0) C、(-5,0) D、(0,-5)5. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间6. 在某次试验中,测得两个变量 和 之间的4组对应数据如下表:1
2
3
4
0
3
8
15
则 与 之间的关系满足下列关系式( )
A、 B、 C、 D、7. 实数 在数轴上的位置如图所示,化简 的结果是( )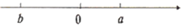 A、 B、 C、 D、8. 能表示一次函数y=mx+n与正比例函数y=mnx(m , n是常数且m≠0)的图象的是( )A、
A、 B、 C、 D、8. 能表示一次函数y=mx+n与正比例函数y=mnx(m , n是常数且m≠0)的图象的是( )A、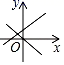 B、
B、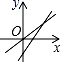 C、
C、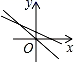 D、
D、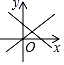
二、填空题
-
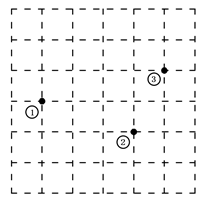
9. 如图所示的棋盘放置在某个平面直角坐标系内,棋子①的坐标为 ,棋子②的坐标为 ,那么棋子③的坐标是.
 10. 已知一个直角三角形的两边长分别为12和5,则第三条边的长度为11. 当 时,函数 是一次函数。12. 已知点在第四象限,且点P到x轴的距离为5,到y轴的距离为2,那么点P的坐标为 .13. 已知一次函数 同时满足下列两个条件:①图象经过点 ;②函数值 随 的增大而增大。请你写出符合要求的一次函数关系式(写出一个即可)14. 如图,有一个三级台阶,它的每一级的长, 宽和高分别是 , , ,点 和点 是这个台阶两个相对的端点, 点有一只蚂蚁,想到 点去吃可口的食物,则蚂蚁沿着台阶表面爬到 点的最短路程是 .
10. 已知一个直角三角形的两边长分别为12和5,则第三条边的长度为11. 当 时,函数 是一次函数。12. 已知点在第四象限,且点P到x轴的距离为5,到y轴的距离为2,那么点P的坐标为 .13. 已知一次函数 同时满足下列两个条件:①图象经过点 ;②函数值 随 的增大而增大。请你写出符合要求的一次函数关系式(写出一个即可)14. 如图,有一个三级台阶,它的每一级的长, 宽和高分别是 , , ,点 和点 是这个台阶两个相对的端点, 点有一只蚂蚁,想到 点去吃可口的食物,则蚂蚁沿着台阶表面爬到 点的最短路程是 .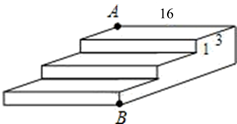 15. 一个数的算术平方根为 ,平方根为 ,则这个数是.16. 在平面直角坐标系中, 的位置如图所示,其中点 为坐标原点, , ,则点 关于 轴对称的点的坐标是.
15. 一个数的算术平方根为 ,平方根为 ,则这个数是.16. 在平面直角坐标系中, 的位置如图所示,其中点 为坐标原点, , ,则点 关于 轴对称的点的坐标是.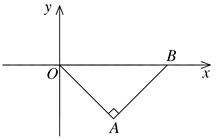
三、解答题
-
17. 计算(1)、(2)、(3)、(4)、18. 如图,正方形网格中每个小正方形的边长都是1,小正方形的顶点叫格点,以格点为顶点画一个直角三角形,使其面积为4,且至少有两边长为无理数.
 19. 如图,已知 。求图中阴影部分的面积。
19. 如图,已知 。求图中阴影部分的面积。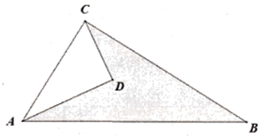 20. 某一品牌的乒乓球在甲、乙两个商场的标价都是每个3元,在销售时都有一定的优惠。甲商场的优惠条件是购买不超过10个按原价销售,超过10个,超出部分按8折优惠;乙商场的优惠条件是无论买多少个都按9折优惠。(1)、分别写出在甲、乙两个商场购买这种乒乓球应付金额 元与购买个数 个之间的函数关系式;(2)、若要购买30个乒乓球,到哪家商场购买合算?请说明理由。21. 一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为 (小时),两车之间的距离为 (千米),图中的折线表示 与 之间的函数关系。
20. 某一品牌的乒乓球在甲、乙两个商场的标价都是每个3元,在销售时都有一定的优惠。甲商场的优惠条件是购买不超过10个按原价销售,超过10个,超出部分按8折优惠;乙商场的优惠条件是无论买多少个都按9折优惠。(1)、分别写出在甲、乙两个商场购买这种乒乓球应付金额 元与购买个数 个之间的函数关系式;(2)、若要购买30个乒乓球,到哪家商场购买合算?请说明理由。21. 一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为 (小时),两车之间的距离为 (千米),图中的折线表示 与 之间的函数关系。根据图象回答下列问题:
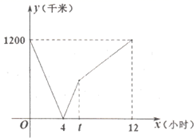 (1)、甲地与乙地相距千米,两车出发后小时相遇;(2)、普通列车到达终点共需小时,普通列车的速度是千米/小时;(3)、动车的速度是千米/小时;(4)、t的值为.22. 如图,在长方形 中,点 在边 上,把长方形 沿直线 折叠,点 落在边 上的点 处。若 .
(1)、甲地与乙地相距千米,两车出发后小时相遇;(2)、普通列车到达终点共需小时,普通列车的速度是千米/小时;(3)、动车的速度是千米/小时;(4)、t的值为.22. 如图,在长方形 中,点 在边 上,把长方形 沿直线 折叠,点 落在边 上的点 处。若 .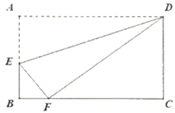 (1)、求 的长;(2)、求 的面积。23. 我们已经知道,形如 的无理数的化简要借助平方差公式:
(1)、求 的长;(2)、求 的面积。23. 我们已经知道,形如 的无理数的化简要借助平方差公式:例如: 。
下面我们来看看完全平方公式在无理数化简中的作用。
问题提出: 该如何化简?
建立模型:形如 的化简,只要我们找到两个数 ,使 ,这样 , ,那么便有: ,
问题解决:化简 ,
解:首先把 化为 ,这里 , ,由于4+3=7, ,
即( , ,
∴
模型应用1:
利用上述解决问题的方法化简下列各式:
(1)、 ;(2)、 ;模型应用2:
(3)、在 中, , , ,那么 边的长为多少?(结果化成最简)。24. 如图,一次函数 的图象分别与 轴和 轴交于 , 两点,且与正比例函数 的图象交于点 .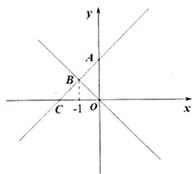 (1)、求 的值;(2)、求正比例函数的表达式;(3)、点 是一次函数图象上的一点,且 的面积是3,求点 的坐标;(4)、在 轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由.
(1)、求 的值;(2)、求正比例函数的表达式;(3)、点 是一次函数图象上的一点,且 的面积是3,求点 的坐标;(4)、在 轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由.