广西壮族自治区玉林市陆川县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
1. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、2. 在 中, ,则 ( )A、 B、 C、 D、3. 下图中,不是函数图象的是( )A、
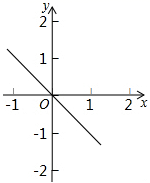 B、
B、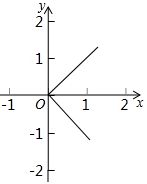 C、
C、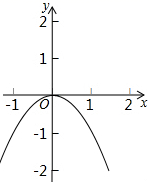 D、
D、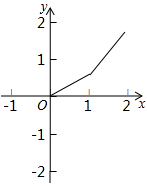 4. 下列四组线段中,能组成直角三角形三条边的是( )A、 , , B、 , , C、 , , D、 , ,5. 已知:x1 , x2 , x3...x10的平均数是a,x11 , x12 , x13...x50的平均数是b,则x1 , x2 , x3...x50的平均数是( )A、a+b B、 C、 D、6. 如图,菱形 的两条对角线相交于点O,若 , ,则菱形 的面积是( )
4. 下列四组线段中,能组成直角三角形三条边的是( )A、 , , B、 , , C、 , , D、 , ,5. 已知:x1 , x2 , x3...x10的平均数是a,x11 , x12 , x13...x50的平均数是b,则x1 , x2 , x3...x50的平均数是( )A、a+b B、 C、 D、6. 如图,菱形 的两条对角线相交于点O,若 , ,则菱形 的面积是( )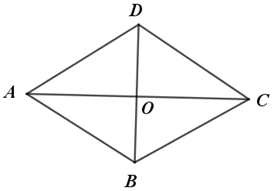 A、24 B、16 C、12 D、107. 矩形,菱形,正方形都具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角8. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=kx+k的图象大致是( )A、
A、24 B、16 C、12 D、107. 矩形,菱形,正方形都具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线平分一组对角8. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=kx+k的图象大致是( )A、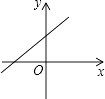 B、
B、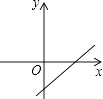 C、
C、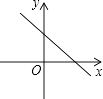 D、
D、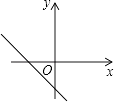 9. 根据表中一次函数的自变量x与函数y的对应值,可得表中p的值为( )
9. 根据表中一次函数的自变量x与函数y的对应值,可得表中p的值为( )1
3
0
A、2 B、 C、0 D、110. 5个整数从小到大的排列,其中位数是4,如果这组数据的唯一众数是6,则这5个整数最大的和可能是( )A、 21 B、22 C、23 D、2411. 如图,直线 与 的交点的横坐标为-2,则关于x的不等式 的整数解为( ).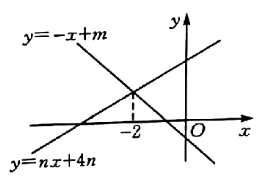 A、 B、 C、 D、12. 如图,矩形 中,O为 中点,过点O的直线分别与 , 交于点E,F,连接 交 于点M,连接 , .若 , ,则下列结论:
A、 B、 C、 D、12. 如图,矩形 中,O为 中点,过点O的直线分别与 , 交于点E,F,连接 交 于点M,连接 , .若 , ,则下列结论:① , ;
② ;
③四边形 是菱形;
④ .
其中正确结论的个数是( )
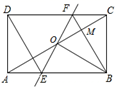 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 要使二次根式 有意义,则x的取值范围是 .
14. 将正比例函数 的图象向上平移3个单位,则平移后所得图象的解析式是.15. 在湖的两侧有A,B两个消防栓,为测定它们之间的距离,小东在岸上任选一点C,并量取了 中点D和 中点E之间的距离为18米,则A,B之间的距离为米. 16. a,b,c是 的三边长,满足关系式 ,则 的形状为.17. 如图,在菱形 中, 的垂直平分线 交对角线 于点F,垂足为点E,若 ,则 的度数为.
16. a,b,c是 的三边长,满足关系式 ,则 的形状为.17. 如图,在菱形 中, 的垂直平分线 交对角线 于点F,垂足为点E,若 ,则 的度数为.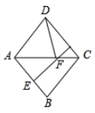 18. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元.
18. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元.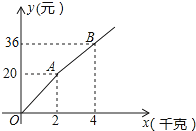
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 先化简,再求值: ,其中a= .21. 为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数
中位数
方差
命中10环的次数
甲
7
7
0
乙
7
5.4
1
甲、乙射击成绩折线图
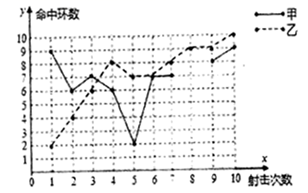 (1)、请补全上述图表(请直接在统计表中填空和补全折线图);(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由.22. 在一节数学课上,老师布置了一个任务:
(1)、请补全上述图表(请直接在统计表中填空和补全折线图);(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由.22. 在一节数学课上,老师布置了一个任务:已知,如图1,在 中, ,用尺规作图作矩形 .
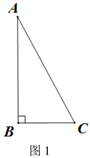

同学们开动脑筋,想出了很多办法,其中小亮作了图2,他向同学们分享了作法:
①分别以点A、C为圆心,大于 长为半径画弧,两弧分别交于点E、F,连接 交 于点O;
②作射线 ,在 上取点D,使 ;
③连接 , .
则四边形 就是所求作的矩形.
老师说:“小亮的作法正确.”
写出小亮的作图依据.
23. 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米?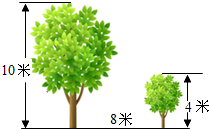 24. 已知点 及在第一象限的动点 ,且 , 为坐标原点,设 的面积为S.
24. 已知点 及在第一象限的动点 ,且 , 为坐标原点,设 的面积为S.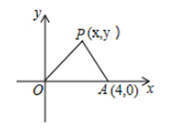 (1)、求S关于x的函数解析式;(2)、直接写出x的取值范围;(3)、当 时,求P点的坐标.25. 为改善生态环境,防止水土流失,某村计划在九洲江堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
(1)、求S关于x的函数解析式;(2)、直接写出x的取值范围;(3)、当 时,求P点的坐标.25. 为改善生态环境,防止水土流失,某村计划在九洲江堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:甲林场
购树苗数量
销售单价
不超过1000棵时
4元/棵
超过1000棵的部分
3.8元/棵
乙林场
购树苗数量
销售单价
不超过2000棵时
4元/棵
超过2000棵的部分
3.6元/棵
设购买白杨树苗x棵,到两家林场购买所需费用分别为 (元), (元).
(1)、该村需要购买1800棵白杨树苗,如果都在甲林场购买所需费用为元,如果都在乙林场购买所需费用为元;(2)、分别求出 , 与x之间的函数关系式;(3)、如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?26. 如图,在 中, , , ,点D从点C出发沿 方向以 秒的速度向点A匀速运动,同时点E从点A出发沿 方向以 秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是 秒( ).过点D作 于点F,连接 , .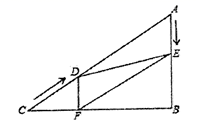 (1)、求证: ;(2)、当 时,四边形 是什么四边形?请说明理由(3)、在运动过程中,四边形 能否为正方形?若能,求出t的值;若不能,请说明理由.
(1)、求证: ;(2)、当 时,四边形 是什么四边形?请说明理由(3)、在运动过程中,四边形 能否为正方形?若能,求出t的值;若不能,请说明理由.