山东省济宁市邹城市2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列说法中错误的是（）

A、三角形的中线一定在三角形内部 B、三角形的高不一定在三角形内部 C、三角形的外角一定大于它的内角 D、一个三角形中至少有一个角不小于 $60 °$

查看试题解析
3. 等腰三角形的一个外角等于 $70 °$ ，则它的底角是（）

A、110° B、55° C、35° D、35°或55°

查看试题解析
4. 如图，将△ABC的三个顶点坐标的横坐标都乘以-1，并保持纵坐标不交，则所得图形与原图形的关系是（）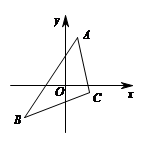

A、关于x轴对称 B、关于y轴对称 C、将原图形沿x轴的负方向平移了1个单位 D、将原图形沿y轴的负方向平移了1个单位

查看试题解析
5. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D，E可在槽中滑动，若∠BDE=75°，则∠CDE的度数是（）

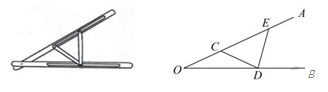A、60° B、65° C、75° D、80°

查看试题解析
6.
如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（　　）

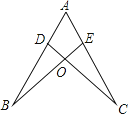A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD

查看试题解析
7. 如图， $C D$ 是 $Δ A B C$ 的角平分线， $A E ⊥ C D$ 交 $B C$ 于点 $E$ ．若 $∠ B = 45 °$ ， $∠ A C B = 55 °$ ，则 $∠ B D E$ 的度数为（）

A、25° B、35° C、40° D、45°

查看试题解析
8. 在平面直角坐标系中，点A（2，0），B（0，4），若以B，O，C为顶点的三角形与△ABO全等，则点C的坐标不能为（）

A、（0，﹣4） B、（﹣2，0） C、（2，4） D、（﹣2，4）

查看试题解析
9. 如图， $Δ A B C$ 中， $A D$ 是角平分线， $B E$ 是 $Δ A B D$ 中的中线，若 $Δ A B C$ 的面积是 $24$ ， $A B = 5$ ， $A C = 3$ ，则 $Δ A B E$ 的面积是（）

A、15 B、12 C、7.5 D、6

查看试题解析
10. 已知n正整数，若一个三角形的三边长分别是n+2、n+8、3n，则满足条件的n的值有（）

A、4个 B、5个 C、6个 D、7个

查看试题解析

二、填空题

11. 正十边形的外角和为．

查看试题解析
12. 若等腰三角形的一边长等于 $6$ ，另一边长等于 $3$ ，则它的周长等于.

查看试题解析
13. 已知点 $A (5, m - 1)$ 和点 $B (n + 1, 2)$ 关于 $y$ 轴成轴对称，则 $m + n =$ ．

查看试题解析
14. 如图，在 $Δ A B C$ 中， $A B$ 的垂直平分线 $D E$ 交 $B C$ 于点 $D$ ，若 $A C = A D$ ， $∠ C = 50 °$ ，则 $∠ B$ 的度数为．

查看试题解析
15. 如图， $Δ A B C$ 中， $D$ ， $E$ 分别是边 $A B$ ， $A C$ 上的点， $D E$ 的延长线交过 $C$ 点的 $A B$ 的平行线于点 $F$ ．若 $D E = F E$ ， $A B = 5$ ， $C F = 3$ ，则 $B D$ 的长是．

查看试题解析
16. 如图， $Δ A O C$ 和 $Δ A O B$ 关于直线 $A O$ 对称， $Δ D O B$ 和 $Δ A O B$ 关于直线 $B O$ 对称， $O C$ 与 $B D$ 交于点 $E$ ，若 $∠ C = 15 °$ ， $∠ D = 25 °$ ，则 $∠ B E C$ 的度数为．

查看试题解析
17. 在平面直角坐标系中，点 $A$ 在 $x$ 轴的正半轴上，点 $B$ 在 $y$ 轴的正半轴上， $∠ A B O = 36 °$ ，在 $x$ 轴或 $y$ 轴上取点 $C$ ，使得 $Δ A B C$ 为等腰三角形，符合条件的 $C$ 点有个．

查看试题解析
18. 如图，在 $Δ A B C$ 中， $∠ B A C = 120 °$ ， $A B = 4$ ， $D$ 为 $B C$ 的中点， $A D ⊥ A B$ ，则 $A C$ 的长为．

查看试题解析

三、解答题

19. 已知：在如图所示的“风筝”图案中，AB＝AD，∠C＝∠E，∠BAE＝∠DAC.求证：AC＝AE.

查看试题解析
20. 如图

(1)、如图1，在平面直角坐标系中， $Δ A B C$ 的顶点为 $A (- 3 ， - 2)$ ， $B (3 ， 1)$ ， $C (1 ， 4)$ ．画出 $Δ A B C$ 关于 $x$ 轴的对称图形 $Δ A_{1} B_{1} C_{1}$ ；

(2)、如图2， $Δ D E F$ 中， $∠ E = 90 °$ ．请用直尺和圆规作一条直线，把 $Δ D E F$ 分割成两个等腰三角形（不写作法，但须保留作图痕迹）．

查看试题解析
21. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．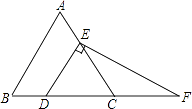

(1)、求∠F的度数；

(2)、若CD=2，求DF的长．

查看试题解析
22. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $A D$ 是中线，过 $C$ 点作 $A D$ 的平行线交 $B A$ 的延长线于点 $E$ ．

(1)、求证： $Δ A C E$ 为等腰三角形；

(2)、延长 $C A$ 至点 $F$ ，使 $A F = A C$ ，连接 $B F$ ，求证： $B F ⊥ B C$ ．

查看试题解析
23. 已知 $Δ A B C$ 和 $Δ D E F$ 都是等腰直角三角形， $∠ B A C = ∠ E D F = 90 °$ ，点 $D$ 是 $B C$ 的中点，连接 $A E$ ， $B F$ ．

(1)、当点 $A$ ， $C$ 分别在 $D F$ 和 $D E$ 上时，如图1，试猜想线段 $A E$ 和 $B F$ 的数量关系，请直接写出你得到的结论（不要求证明）；

(2)、将 $Δ D E F$ 绕点 $D$ 逆时针方向旋转一定角度后（旋转角度大于 $0 °$ ，小于或等于 $360 °$ ），如图2，请问：（1）中的结论是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．

查看试题解析
24. 如图，在 $Δ A B C$ 中，点 $M$ 在 $A B$ 上， $C N / / A B$ ， $B M = C N$ ， $M N$ 交 $B C$ 于点 $D$ ，过点 $D$ 作 $B C$ 的垂线交 $A B$ 于点 $P$ ，连接 $P C$ ．

(1)、求证： $P B = P C$ ；

(2)、连接 $P N$ 交 $B C$ 于点 $E$ ，已知 $∠ C N P = 2 ∠ C P N$ ，求证： $E N = P M$ ．

查看试题解析