山东省济宁市任城区2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-27 类型：期中考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{2}{x - 3}$ 有意义，则x应满足的条件是（）

A、x≠0 B、x≥3 C、x≠3 D、x≤3

查看试题解析
2. 下列各式中不是分式的是（）

A、 $\frac{2 x}{x + y}$ B、 $\frac{1}{π^{2}}$ C、 $\frac{1}{x^{2}}$ D、 $\frac{x^{3}}{x - 1}$

查看试题解析
3. 下列由左到右的变形中属于因式分解的是（）

A、24x²y＝3x•8xy B、m²﹣2m﹣3＝m（m﹣2）﹣3 C、m²﹣2m﹣3＝（m﹣3）（m+1） D、（x+3）（x﹣3）＝x²﹣9

查看试题解析
4. 某校5名同学在“国学经典颂读”比赛中，成绩（单位：分）分别是86，95，97，90，88，这组数据的中位数是（）

A、97 B、90 C、95 D、88

查看试题解析
5. 利用因式分解计算： $2^{100} - 2^{101} =$ （）

A、-2 B、2 C、 $2^{100}$ D、 $- 2^{100}$

查看试题解析
6. 若把分式 $\frac{2 x y}{x + y}$ 的x、y同时扩大3倍，则分式值（）

A、不变 B、扩大为原来的3倍 C、缩小为原来的 $\frac{1}{3}$ D、扩大为原来的9倍

查看试题解析

7. 一次数学测试，某小组

5

名同学的成绩统计如下（有两个数据被遮盖）：

组员	甲	乙	丙	丁	戊	平均成绩	众数
得分	$81$	$77$	■	$80$	$82$	$80$	■

则被遮盖的两个数据依次是（）

A、

80, 80

B、

81, 80

C、

80, 2

D、

81, 2

查看试题解析

8. 从甲地到乙地有两条同样长的路，一条是平路，另一条的 $\frac{1}{3}$ 是上山， $\frac{2}{3}$ 是下山，如果上山的速度为平路速度的 $\frac{1}{2}$ ，平路速度是下山速度的 $\frac{1}{2}$ ，那么从甲地到乙地（）

A、走山路快 B、走平路快 C、走山路与平路一样快 D、哪个快不能确定

查看试题解析
9. 已知a＝2018x＋2018，b＝2018x＋2019，c＝2018x＋2020，则a²＋b²＋c²－ab－ac－bc的值是( )

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

10. 已知 $x^{2} + 4 m x + 16$ 能用完全平方公式因式分解，则 $m$ 的值为.

查看试题解析
11. 一组数据2.2，3.3，4.4，11.1， $a$ .其中整数 $a$ 是这组数据中的中位数，则这组数据的平均数是.

查看试题解析
12. 若x+ $\frac{1}{x}$ =2，则x²+ $\frac{1}{x^{2}}$ = ， x³+ $\frac{1}{x^{3}}$ = ，x⁴+ $\frac{1}{x^{4}}$ = ．任意正整数n，猜想：xⁿ+ $\frac{1}{x^{n}}$ = ．

查看试题解析
13. 关于x的方程 $\frac{2 a x + 3}{a - x} = \frac{3}{4}$ 的解为x=1，则a=.

查看试题解析
14. 观察以下等式：
第1个等式： $\frac{2}{1} = \frac{1}{1} + \frac{1}{1}$ ，

第2个等式： $\frac{2}{3} = \frac{1}{2} + \frac{1}{6}$ ，

第3个等式： $\frac{2}{5} = \frac{1}{3} + \frac{1}{15}$ ，

第4个等式： $\frac{2}{7} = \frac{1}{4} + \frac{1}{28}$ ，

第5个等式： $\frac{2}{9} = \frac{1}{5} + \frac{1}{45}$ ，

……

按照以上规律，写出你猜想的第 $n$ 个等式：（用含 $n$ 的等式表示）.

查看试题解析

三、解答题

15. 分解因式

(1)、 $a^{2} b - b$ ；

(2)、 $- 2 x^{3} + 12 x^{2} - 18 x$

查看试题解析
16. 计算下列各题

(1)、 $(a b - b^{2}) \div \frac{a - b}{a b}$

(2)、 ${(\frac{y}{6 x^{2}})}^{2} \div {(\frac{y^{2}}{4 x})}^{2}$

查看试题解析
17. 解分式方程

(1)、 $\frac{2}{x} = \frac{3}{x + 2}$

(2)、 $\frac{x}{x - 2} - \frac{1}{x^{2} - 4} = 1$

查看试题解析

18. 为了提高学生对毒品危害性的认识，我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性，某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标，该校随机选取了七年级20名学生在5月份测评的成绩，数据如下：

收集数据：90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88

(1)、根据上述数据，将下列表格补充完整.

整理、描述数据：

成绩/分	88	89	90	91	95	96	97	98	99
学生人数	2	1		3	2	1		2	1

数据分析：样本数据的平均数、众数和中位数如下表：

平均数	众数	中位数
93		91

得出结论：

(2)、根据所给数据，如果该校想确定七年级前50%的学生为“良好”等次，你认为“良好”等次的测评成绩至少定为分.

数据应用：

(3)、根据数据分析，该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号，请估计评选该荣誉称号的最低分数，并说明理由.

查看试题解析

19. 学习了因式分解的知识后，老师提出了这样一个问题：设 $n$ 为整数，则 ${(n + 7)}^{2} - {(n - 3)}^{2}$ 的值一定能被20整除吗？若能，请说明理由？若不能，请举出一个反例，你能回答这个问题吗？

查看试题解析
20. 先化简，再从﹣1、2、3、4中选一个合适的数作为x的值代入求值． $(\frac{x^{2} - 2 x}{x^{2} - 4 x + 4} - \frac{4}{x - 2}) \div \frac{x - 4}{x^{2} - 4}$ .

查看试题解析
21. 如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m＞n．（以上长度单位：cm）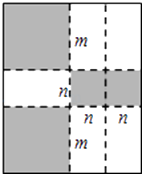

(1)、用含m，n的代数式表示所有裁剪线（图中虚线部分）的长度之和；

(2)、观察图形，发现代数式2m²+5mn+2n²可以因式分解为；

(3)、若每块小矩形的面积为10cm² ，四个正方形的面积和为58cm² ，试求(m+n)²的值．

查看试题解析
22. 为进一步营造扫黑除恶专项斗争的浓厚宣传氛围，推进平安校园建设，甲、乙两所学校各租用一辆大巴车组织部分师生，分别从距目的地240千米和270千米的两地同时出发，前往“研学教育”基地开展扫黑除恶教育活动，已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍，甲校师生比乙校师生晚1小时到达目的地，分别求甲、乙两所学校师生所乘大巴车的平均速度.

查看试题解析
23. 某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

(1)、求甲、乙两种树苗每棵的价格各是多少元？

(2)、在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

查看试题解析