陕西省延安市富县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
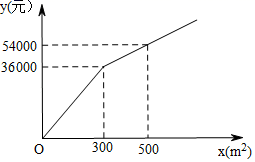
1. 与 是同类二次根式,符合条件的a的值可以是( )A、12 B、14 C、 D、242. 如图,在平行四边形ABCD中,CE⊥AB , E为垂足.如果∠BCE=28°,则∠D=( )
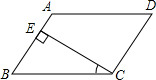 A、28° B、38° C、52° D、62°3. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差,从这四人中选择一名成绩好又发挥稳定的运动员参加决赛,最合适的是( )
A、28° B、38° C、52° D、62°3. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差,从这四人中选择一名成绩好又发挥稳定的运动员参加决赛,最合适的是( )运动员
甲
乙
丙
丁
平均数( )
376
350
376
350
方差
12.5
13.5
2.4
5.4
A、甲 B、乙 C、丙 D、丁4. 下列计算正确的是( )A、 B、 C、 D、5. 已知y关于x成正比例,且当 时, ,则当 时,y的值为( )A、3 B、 C、12 D、6. 在四边形ABCD中,两对角线交于点O,若OA=OB=OC=OD,则这个四边形( )A、可能不是平行四边形 B、一定是菱形 C、一定是正方形 D、一定是矩形7. 已知正比例函数y=kx的图象经过第一、三象限,则一次函数y=kx﹣k的图象可能是下图中的( )A、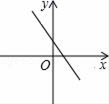 B、
B、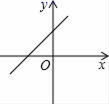 C、
C、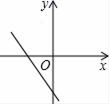 D、
D、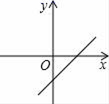 8. 如图,小巷左、右两侧是竖直的墙壁,一架梯子斜靠在左墙上时,梯子底端到左墙角的距离为1米,梯子顶端距离地面3米.若梯子底端位置保持不动,将梯子斜靠在右墙上,此时梯子顶端距离地面2米,则小巷的宽度为 ( )
8. 如图,小巷左、右两侧是竖直的墙壁,一架梯子斜靠在左墙上时,梯子底端到左墙角的距离为1米,梯子顶端距离地面3米.若梯子底端位置保持不动,将梯子斜靠在右墙上,此时梯子顶端距离地面2米,则小巷的宽度为 ( ) A、 米 B、3米 C、 米 D、2米9. 一次函数y=kx+b(k≠0)的图象经过点B(﹣6,0),且与正比例函数y= x的图象交于点A(m , ﹣3),若kx﹣ x>﹣b , 则( )
A、 米 B、3米 C、 米 D、2米9. 一次函数y=kx+b(k≠0)的图象经过点B(﹣6,0),且与正比例函数y= x的图象交于点A(m , ﹣3),若kx﹣ x>﹣b , 则( )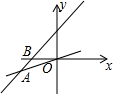 A、x>0 B、x>﹣3 C、x>﹣6 D、x>﹣910. 如图,在 中,以点O为圆心,任意长为半径作弧,交射线 于点C,交射线 于点D,再分别以 为圆心, 的长为半径作弧,两弧在 的内部交于点E,作射线 ,若 ,则 两点之间的距离为( )
A、x>0 B、x>﹣3 C、x>﹣6 D、x>﹣910. 如图,在 中,以点O为圆心,任意长为半径作弧,交射线 于点C,交射线 于点D,再分别以 为圆心, 的长为半径作弧,两弧在 的内部交于点E,作射线 ,若 ,则 两点之间的距离为( )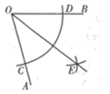 A、10 B、12 C、13 D、8
A、10 B、12 C、13 D、8二、填空题
-
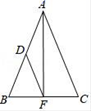
11. 已知 ,则a的倒数是.12. 如图,在△ABC中,AB=AC,BC=6,点F是BC的中点,点D是AB的中点,连接AF和DF,若△DBF的周长是11,则AB=.
 13. 甲、乙两龙舟队举行赛龙舟比赛,两队在比赛过程中的路程y(米)与时间t(分钟)之间的函数关系如图所示,下列结论:①甲队率先到达终点;②甲队比乙队多划200米路程;③划完全程乙队比甲队少用0.2分钟;④比赛过程中当 时,乙队的速度比甲队的速度快.其正确的结论有个.
13. 甲、乙两龙舟队举行赛龙舟比赛,两队在比赛过程中的路程y(米)与时间t(分钟)之间的函数关系如图所示,下列结论:①甲队率先到达终点;②甲队比乙队多划200米路程;③划完全程乙队比甲队少用0.2分钟;④比赛过程中当 时,乙队的速度比甲队的速度快.其正确的结论有个. 14. 如图,D是 内一点, , 分别是 的中点,若 ,则四边形 的周长是.
14. 如图,D是 内一点, , 分别是 的中点,若 ,则四边形 的周长是.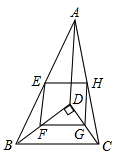
三、解答题
-
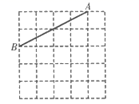
15. 计算: ÷2 +( )( )- .16. 已知关于x的正比例函数 ,求这个正比例函数的解析式.17. 如图,在正方形网格中,每个小正方形的顶点称为格点.画出以 为斜边的直角 ,且 的顶点均在格点上,各边长均为无理数.
 18. 如图,已知菱形 的对角线 与 相交于点 , ,求菱形 的周长.
18. 如图,已知菱形 的对角线 与 相交于点 , ,求菱形 的周长.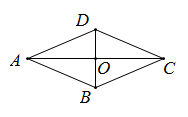 19. 某体育协会为了解青少年足球运动员的年龄情况,做了一次年龄(单位:岁)调查,并将调查结果绘制成了如下的统计图①和图②.请根据相关信息,解答下列问题:
19. 某体育协会为了解青少年足球运动员的年龄情况,做了一次年龄(单位:岁)调查,并将调查结果绘制成了如下的统计图①和图②.请根据相关信息,解答下列问题: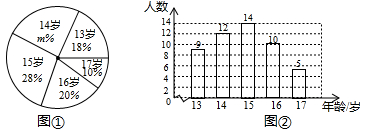 (1)、本次被调查的青少年足球运动员人数为 , 图①中 ;(2)、求被调查的青少年足球运动员年龄的平均数、众数和中位数.20. 一次函数 的图象与x轴交与点 ,(1)、求出a的值;(2)、将该一次函数的图象向上平移 个单位长度,求平移后的函数解析式.21. 某校将从行规、学风、纪律三个方面对甲、乙两个班的综合情况进行评估,各项成绩均按百分制计.各班三个项目的得分情况如下表:
(1)、本次被调查的青少年足球运动员人数为 , 图①中 ;(2)、求被调查的青少年足球运动员年龄的平均数、众数和中位数.20. 一次函数 的图象与x轴交与点 ,(1)、求出a的值;(2)、将该一次函数的图象向上平移 个单位长度,求平移后的函数解析式.21. 某校将从行规、学风、纪律三个方面对甲、乙两个班的综合情况进行评估,各项成绩均按百分制计.各班三个项目的得分情况如下表:行规
学风
纪律
甲班
83分
88分
90分
乙班
93分
86分
84分
该校认为这三个项目的重要程度有所不同,行规、学风、纪律三个项目在总成绩中所占的百分比分别为20%、30%、50%,哪个班级较优秀?
22. 如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.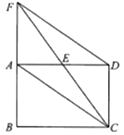 (1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.23. 如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了 m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C.
(1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.23. 如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了 m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C.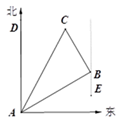 (1)、求A、C两点之间的距离;(2)、确定目的地C在营地A的北偏东多少度方向.
(1)、求A、C两点之间的距离;(2)、确定目的地C在营地A的北偏东多少度方向.