山东省德州市禹城市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列图形是轴对称图形的有( )
 A、2个 B、3个 C、4个 D、5个2. 下面各组线段中,能组成三角形的是( )A、5,11,6 B、6,9,14 C、10,5,4 D、8,8,163. 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )
A、2个 B、3个 C、4个 D、5个2. 下面各组线段中,能组成三角形的是( )A、5,11,6 B、6,9,14 C、10,5,4 D、8,8,163. 如图,是三个等边三角形随意摆放的图形,则∠1+∠2+∠3等于( )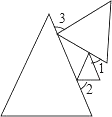 A、90° B、120° C、150° D、180°4. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、90° B、120° C、150° D、180°4. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
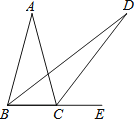
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD5. 已知∠AOB=30°,点P在∠AOB内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2的形状一定是( )A、直角三角形 B、等边三角形 C、底边和腰不相等的等腰三角形 D、钝角三角形6. 如图,AB∥CD , BP和CP分别平分∠ABC和∠DCB , AD过点P , 且与AB垂直.若AD=8,则点P到BC的距离是( )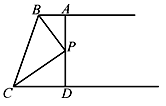 A、8 B、6 C、4 D、27.
A、8 B、6 C、4 D、27.如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
 A、15° B、17.5° C、20° D、22.5°8. △ABC中,∠ABC与∠ACB的平分线相交于I,且∠BIC=130°,则∠A的度数是( )A、 B、 C、 D、9.
A、15° B、17.5° C、20° D、22.5°8. △ABC中,∠ABC与∠ACB的平分线相交于I,且∠BIC=130°,则∠A的度数是( )A、 B、 C、 D、9.如图,直线a、b、c、d互不平行,对它们截出的一些角的数量关系描述错误的是( )
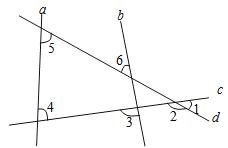 A、∠1+∠6﹦∠2 B、∠4+∠5﹦∠2 C、∠1+∠3+∠6﹦180° D、∠1+∠5+∠4﹦180°10. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为( )
A、∠1+∠6﹦∠2 B、∠4+∠5﹦∠2 C、∠1+∠3+∠6﹦180° D、∠1+∠5+∠4﹦180°10. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=10°,则∠C的度数为( ) A、30° B、40° C、50° D、60°11. 如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A、30° B、40° C、50° D、60°11. 如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )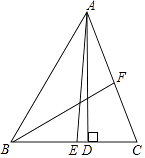 A、75° B、80° C、85° D、90°12. 如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A、75° B、80° C、85° D、90°12. 如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13.
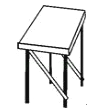
如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
 14. 点A(3,-2)关于x轴对称的点的坐标是 .15. 等腰三角形的一个角是50°,则它的底角为°.16. 若n边形的内角和是它的外角和的2倍,则n=.17. 如图所示,顶角A为120°的等腰△ABC中,DE垂直平分AB于D , 若DE=2,则EC= .
14. 点A(3,-2)关于x轴对称的点的坐标是 .15. 等腰三角形的一个角是50°,则它的底角为°.16. 若n边形的内角和是它的外角和的2倍,则n=.17. 如图所示,顶角A为120°的等腰△ABC中,DE垂直平分AB于D , 若DE=2,则EC= .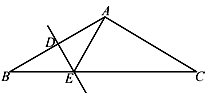 18. 如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= .
18. 如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= .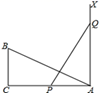
三、解答题
-
19. 如图,在直角坐标系中,先描出点 ,点 .
 (1)、描出点A关于x轴的对称点 的位置,写出 的坐标;(2)、用尺规在x轴上找一点C,使 的值最小(保留作图痕迹);(3)、用尺规在x轴上找一点P,使 (保留作图痕迹).20. 如图, 是等腰三角形, , .
(1)、描出点A关于x轴的对称点 的位置,写出 的坐标;(2)、用尺规在x轴上找一点C,使 的值最小(保留作图痕迹);(3)、用尺规在x轴上找一点P,使 (保留作图痕迹).20. 如图, 是等腰三角形, , .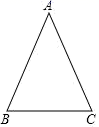 (1)、尺规作图:作 的角平分线 ,交 于点 (保留作图痕迹,不写作法);(2)、判断 是否为等腰三角形,并说明理由.21.
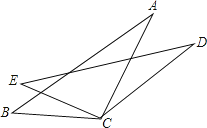
(1)、尺规作图:作 的角平分线 ,交 于点 (保留作图痕迹,不写作法);(2)、判断 是否为等腰三角形,并说明理由.21.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.
 22. 已知:如图,AB=AC,BD=CD,DE⊥AB,垂足为E,DF⊥AC,垂足为F.求证:DE=DF.
22. 已知:如图,AB=AC,BD=CD,DE⊥AB,垂足为E,DF⊥AC,垂足为F.求证:DE=DF.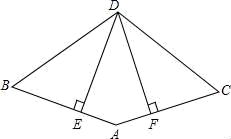 23. 如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC .
23. 如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC .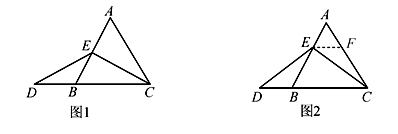 (1)、当点E为AB的中点时(如图1),则有AEDB(填“>”“<”或“=”);(2)、猜想AE与DB的数量关系,并证明你的猜想.24. 如图
(1)、当点E为AB的中点时(如图1),则有AEDB(填“>”“<”或“=”);(2)、猜想AE与DB的数量关系,并证明你的猜想.24. 如图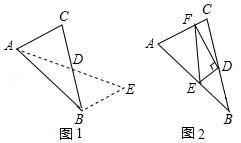 (1)、阅读理解:
(1)、阅读理解:如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是.
(2)、问题解决:如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF.25. 如图①,已知等腰直角 中,BD为斜边上的中线,E为DC上的一点,且 于G,AG交BD于F.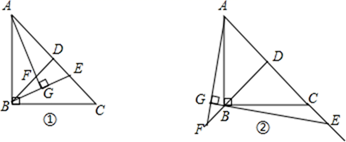 (1)、求证:AF=BE.(2)、如图②,当点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。
(1)、求证:AF=BE.(2)、如图②,当点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。