辽宁省营口市大石桥市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
1. 下列根式中属于最简二次根式的是( )A、 B、 C、 D、2. 下列各数为边不能组成直角三角形的一组是( )A、15,12,9 B、 ,2, C、8,15,17 D、 ,2,3. 下列计算或化简正确的是( )A、 B、 C、 D、4. 已知正比例函数y=kx的函数值y随x的增大而增大,则一次函数y=x﹣k的图象是( )A、
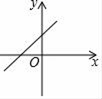 B、
B、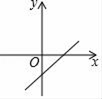 C、
C、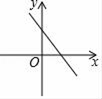 D、
D、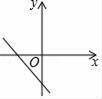 5. 点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数被墨水涂污看不到了,计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数6. 下列判定正确的是( )A、对角线互相垂直的四边形是菱形 B、两条对角线相等且互相垂直的四边形是正方形 C、四边相等且有一个角是直角的四边形是正方形 D、一组对边平行,一组对边相等的四边形是平行四边形7. 下列计算正确的是( )A、 B、 C、 D、8. 如图,在矩形ABCD中对角线AC与BD相交于点O, ,垂足为点E, ,且 ,则AD的长为( )
5. 点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数被墨水涂污看不到了,计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数6. 下列判定正确的是( )A、对角线互相垂直的四边形是菱形 B、两条对角线相等且互相垂直的四边形是正方形 C、四边相等且有一个角是直角的四边形是正方形 D、一组对边平行,一组对边相等的四边形是平行四边形7. 下列计算正确的是( )A、 B、 C、 D、8. 如图,在矩形ABCD中对角线AC与BD相交于点O, ,垂足为点E, ,且 ,则AD的长为( )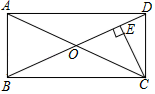 A、 B、 C、10 D、9. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为( )
A、 B、 C、10 D、9. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为( )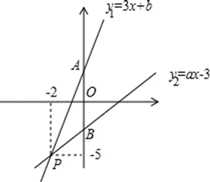 A、x>﹣2 B、x<﹣2 C、x>﹣5 D、x<﹣510. 如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
A、x>﹣2 B、x<﹣2 C、x>﹣5 D、x<﹣510. 如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B C
C  D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积  与点P运动的路程
与点P运动的路程  之间的函数图象大致是( ).
之间的函数图象大致是( ).  A、
A、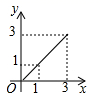 B、
B、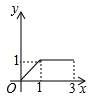 C、
C、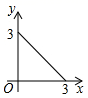 D、
D、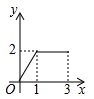
二、填空题
-
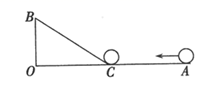
11. 函数 中,自变量x的取值范围是.12. 如图, , , ,一机器人在点B处看见一个小球从点A出发沿着 方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,则机器人行走的路程BC为.
 13. 如图所示,将两张等宽的长方形条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则四边形ABCD的面积是cm2 .
13. 如图所示,将两张等宽的长方形条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则四边形ABCD的面积是cm2 .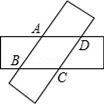 14. 如图,平行四边形 的对角线AC与BD相较于点O, ,垂足为 , , , ,则 的长为.
14. 如图,平行四边形 的对角线AC与BD相较于点O, ,垂足为 , , , ,则 的长为.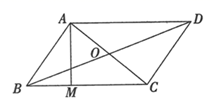 15. 若数据1,4, ,9,6,5的平均数为5.则中位数是;众数是.
15. 若数据1,4, ,9,6,5的平均数为5.则中位数是;众数是.
16. 李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是升.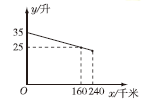 17. 若点P( 1,y1)和点Q( 2,y2)是一次函数y= x+b的图象上的两点,则y1 , y2的大小关系是.18. 矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为.
17. 若点P( 1,y1)和点Q( 2,y2)是一次函数y= x+b的图象上的两点,则y1 , y2的大小关系是.18. 矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为.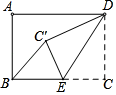
三、解答题
-
19.(1)、(2)、20. 已知:在 中,AD是BC边上的中线,点E是AD的中点;过点A作 ,交BE的延长线于F,连接CF.
 (1)、求证:四边形ADCF是平行四边形;(2)、填空:
(1)、求证:四边形ADCF是平行四边形;(2)、填空:当 时,四边形ADCF是形;
当 时,四边形ADCF是形
21. 有一块空白地,如图,∠ADC=90°,CD=6 m,AD=8 m,AB=26 m,BC=24 m.试求这块空白地的面积. 22. 如图,一次函数 与正比例函数 的图象交于点M.
22. 如图,一次函数 与正比例函数 的图象交于点M.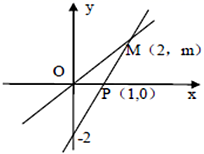 (1)、求正比例函数和一次函数的解析式;(2)、根据图象,写出关于x的不等式 的解集;(3)、求 的面积.23. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
(1)、求正比例函数和一次函数的解析式;(2)、根据图象,写出关于x的不等式 的解集;(3)、求 的面积.23. 某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:完成作业
单元测试
期末考试
小张
70
90
80
小王
60
75
(1)、若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;(2)、若按完成作业、单元检测、期末考试三项成绩按 的权重来确定期末评价成绩.①请计算小张的期末评价成绩为多少分?
②小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
24. △ABC中,点O是AC上一动点,过点O作直线MN BC,若MN交∠BCA的平分线于点E,交∠DCA的平分线于点F,连接AE、AF.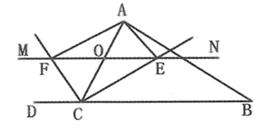 (1)、说明: ;(2)、当点O运动到AC中点处时,求证:四边形AECF是矩形;(3)、在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并加以证明.25. 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、说明: ;(2)、当点O运动到AC中点处时,求证:四边形AECF是矩形;(3)、在(2)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并加以证明.25. 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: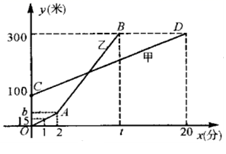 (1)、甲登山的速度是每分钟米,乙在A地提速时距地面的高度b为米.(2)、若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、登山多长时间时,乙追上了甲?此时乙距A地的高度为多少米?
(1)、甲登山的速度是每分钟米,乙在A地提速时距地面的高度b为米.(2)、若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、登山多长时间时,乙追上了甲?此时乙距A地的高度为多少米?