江西省上饶市余干县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列图形:
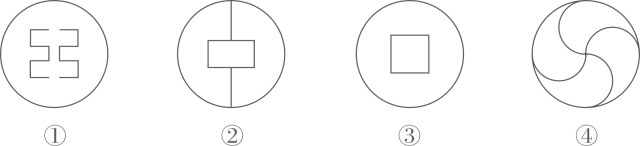
其中是轴对称图形且有两条对称轴的是( )
A、①② B、②③ C、②④ D、③④2. 一个三角形的两边长分别是3和7,则第三边长可能是( )A、2 B、3 C、9 D、103. 下列图形中,正确画出AC边上的高的是( )。A、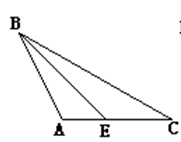 B、
B、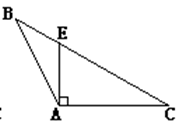 C、
C、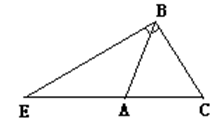 D、
D、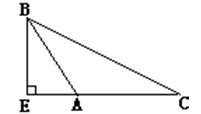 4. 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A’MN,连结A’C,则A’C长度的最小值是( ).
4. 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A’MN,连结A’C,则A’C长度的最小值是( ). A、 B、 C、 D、25. 已知等腰三角形的一边长为3cm,且它的周长为12cm,则它的底边长为( )A、3cm B、6cm C、9cm D、3cm或6cm6.
A、 B、 C、 D、25. 已知等腰三角形的一边长为3cm,且它的周长为12cm,则它的底边长为( )A、3cm B、6cm C、9cm D、3cm或6cm6.小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带( )去.
 A、第1块 B、第2块 C、第3块 D、第4块7. 如图,用等式表示∠1、∠2、∠3与∠4之间的数量关系正确的是( )
A、第1块 B、第2块 C、第3块 D、第4块7. 如图,用等式表示∠1、∠2、∠3与∠4之间的数量关系正确的是( ) A、∠1+∠2+∠3+∠4=360° B、∠1+∠2+∠3=360°+∠4 C、∠1+∠2=∠3﹣∠4 D、∠1+∠2=∠3+∠48. 适合条件∠A= ∠B= ∠C的△ABC是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形9. 已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )A、50° B、80° C、50°或80° D、40°或65°10. 如图,在△ABC中,∠A=78°,∠ACD是△ABC的一个外角,∠EBC= ∠ABC,∠ECD= ∠ACD,则∠E为( )
A、∠1+∠2+∠3+∠4=360° B、∠1+∠2+∠3=360°+∠4 C、∠1+∠2=∠3﹣∠4 D、∠1+∠2=∠3+∠48. 适合条件∠A= ∠B= ∠C的△ABC是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形9. 已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为( )A、50° B、80° C、50°或80° D、40°或65°10. 如图,在△ABC中,∠A=78°,∠ACD是△ABC的一个外角,∠EBC= ∠ABC,∠ECD= ∠ACD,则∠E为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 从n边形的一个顶点出发有四条对角线,则这个n边形的内角和为度.12. 已知点P(2a+b,b)与P1(8,﹣2)关于y轴对称,则a+b=.13. 如图,△ABC≌△ADE , ∠BAE=110°,∠CAD=10°,∠D=40°.则∠BAC=度,∠E=度.
 14. 如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是 .
14. 如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是 .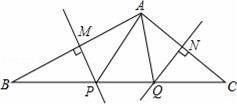 15. 如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: .
15. 如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是: . 16. 如图,三条公路两两相交,现计划修建一个油库,如果要求油库到这三条公路的距离都相等,则油库的位置有个.
16. 如图,三条公路两两相交,现计划修建一个油库,如果要求油库到这三条公路的距离都相等,则油库的位置有个. 17. 如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的角平分线,则∠DAE=度.
17. 如图,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的角平分线,则∠DAE=度. 18. 如果一个多边形是轴对称图形,那么这个多边形可以是(写出一个即可).
18. 如果一个多边形是轴对称图形,那么这个多边形可以是(写出一个即可).三、解答题
-
19. 如图,一辆汽车在笔直的公路AB上由A向B行驶,M , N分别是位于公路AB两侧的村庄,当汽车行驶到哪个位置时,与村庄M , N的距离相等.
 20. 如图,在正方形网格上有一个△ABC.
20. 如图,在正方形网格上有一个△ABC. (1)、画△ABC关于直线MN的对称 (不写画法);(2)、若网格上的每个小正方形的边长为1,求△ABC的面积.21. 如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
(1)、画△ABC关于直线MN的对称 (不写画法);(2)、若网格上的每个小正方形的边长为1,求△ABC的面积.21. 如图,在△ABC中,CD、CE分别是△ABC的高和角平分线. (1)、若∠A=30°,∠B=50°,求∠ECD的度数;(2)、试用含有∠A、∠B的代数式表示∠ECD(不必证明)22. 如图,D、C、F、B四点在一条直线上,AB=DE , AC⊥BD , EF⊥BD , 垂足分别为点C、点F , AC=EF .
(1)、若∠A=30°,∠B=50°,求∠ECD的度数;(2)、试用含有∠A、∠B的代数式表示∠ECD(不必证明)22. 如图,D、C、F、B四点在一条直线上,AB=DE , AC⊥BD , EF⊥BD , 垂足分别为点C、点F , AC=EF .
求证:
(1)、△ABC≌△EDF;(2)、AB∥DE .


