河南省许昌市建安区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
1. 与 是同类二次根式的是( )A、 B、 C、 D、2. 下列关系式中, 不是 的函数的是( )A、 B、 C、 D、3. 圆的面积公式为s=πr2 , 其中变量是( )A、s B、π C、r D、s和r4. 顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )A、正方形 B、矩形 C、菱形 D、梯形5. 一次函数 的图象经过( )A、第一二三象限 B、第二三四象限 C、第一三四象限 D、第一二四象限6. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
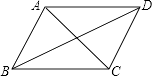 A、当AB=BC时,四边形ABCD是菱形 B、当AC⊥BD时,四边形ABCD是菱形 C、当∠ABC=90°时,四边形ABCD是矩形 D、当AC=BD时,四边形ABCD是正方形7. 根据下表中一次函数的自变量 与 的对应值,可得 的值为( )A、 B、 C、 D、8. 下表记录了甲、乙、丙、丁四名立定跳远运动员选拔赛成绩的平均数与方差:
A、当AB=BC时,四边形ABCD是菱形 B、当AC⊥BD时,四边形ABCD是菱形 C、当∠ABC=90°时,四边形ABCD是矩形 D、当AC=BD时,四边形ABCD是正方形7. 根据下表中一次函数的自变量 与 的对应值,可得 的值为( )A、 B、 C、 D、8. 下表记录了甲、乙、丙、丁四名立定跳远运动员选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数
方差
根据表中数据,要从中选择一名成绩好发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁9. 如图,已知,矩形ABCD中,AB=3 cm,AD=9 cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )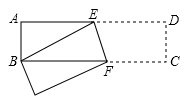 A、3 cm B、4 cm C、5 cm D、 cm10. 有一天,兔子与乌龟赛跑,比赛开始后,兔子飞快地奔跑,乌龟慢慢地爬行,不一会儿,乌龟就被远远地甩在了后面,兔子想:“这比赛也太轻松了,不如先睡一会儿.”而乌龟一刻不停地继续爬行,当兔子醒来跑到终点时,发现乌龟已经到达了终点.能反映这则寓言故事的大致图象是( )A、
A、3 cm B、4 cm C、5 cm D、 cm10. 有一天,兔子与乌龟赛跑,比赛开始后,兔子飞快地奔跑,乌龟慢慢地爬行,不一会儿,乌龟就被远远地甩在了后面,兔子想:“这比赛也太轻松了,不如先睡一会儿.”而乌龟一刻不停地继续爬行,当兔子醒来跑到终点时,发现乌龟已经到达了终点.能反映这则寓言故事的大致图象是( )A、 B、
B、 C、
C、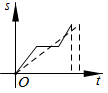 D、
D、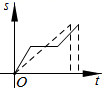
二、填空题
-
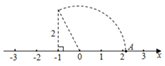
11. 已知正比例函数 ,且 值随 值增大而增大,则 的取值范围是.12. 如图,在数轴上点A表示的实数是.
 13. 如图, 在 中, , , , 为 边上(不与 、 重合的动点过点 分别作 于点 , 于点 , 则线段 的最小值是.
13. 如图, 在 中, , , , 为 边上(不与 、 重合的动点过点 分别作 于点 , 于点 , 则线段 的最小值是. 14. 如图, 正方形 的面积为 , 菱形 的面积为 , 则 的长是.
14. 如图, 正方形 的面积为 , 菱形 的面积为 , 则 的长是.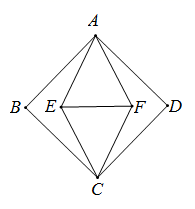 15. 如图,直线 与 轴、 轴分别交于 两点,把 绕点 顺时针旋转 后得到 ,则点 的坐标为 .
15. 如图,直线 与 轴、 轴分别交于 两点,把 绕点 顺时针旋转 后得到 ,则点 的坐标为 .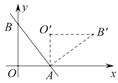
三、解答题
-
16.(1)、计算:(2)、当 , 时,求代数式 的值17. 如图,在四边形 中, , , ,延长 到点 ,使 ,连接
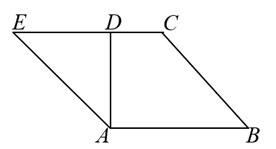 (1)、求证:四边形是 平行四边形(2)、若 , ,求四边形 的面积18. 某校组织了一次低于新冠病毒爱心捐款活动,全体同学积极踊跃捐款,其中随机抽查 名同学捐款情况统计以下:
(1)、求证:四边形是 平行四边形(2)、若 , ,求四边形 的面积18. 某校组织了一次低于新冠病毒爱心捐款活动,全体同学积极踊跃捐款,其中随机抽查 名同学捐款情况统计以下:捐款(元)
人数(人)
求:
(1)、统计捐款数目的众数是 , 中位数是 , 平均数是(2)、请分别用一句话解释本题中的众数、中位数和平均数的意义(3)、若该校捐款学生有 人,估计该校学生-共捐款多少元?19. 如图,已知一次函数 与 的图象相交于点 ,并分别与 轴交于 、 两点
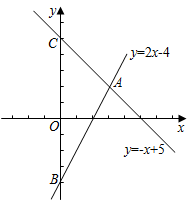 (1)、求交点 的坐标(2)、当 时,求 的取值范围(3)、在 轴上是否存在一点 ,使 ,请写出点 的坐标20. 已知点 及在第一象限的动点 ,且 , 设 的面积为 .(1)、求 关于 的函数解析式,并求出 的取值范围(2)、当 时,求 点的坐标;(3)、画出函数 的图象21. 如图,四边形 是平行四边形, 是 边的中点, ,DF与BC的延长线交于点 , , 的延长线交于点 ,连接 ,若 , , .
(1)、求交点 的坐标(2)、当 时,求 的取值范围(3)、在 轴上是否存在一点 ,使 ,请写出点 的坐标20. 已知点 及在第一象限的动点 ,且 , 设 的面积为 .(1)、求 关于 的函数解析式,并求出 的取值范围(2)、当 时,求 点的坐标;(3)、画出函数 的图象21. 如图,四边形 是平行四边形, 是 边的中点, ,DF与BC的延长线交于点 , , 的延长线交于点 ,连接 ,若 , , . (1)、求线段 的长(2)、试判断直线 与 的位置关系,并说明理由22. 甲乙两家商场以同样价格销售相同的商品,在同一促销期间两家商场都让利酬宾.甲商场所有商品都按原价的八折出售,乙商场只对一次购物中超过100元后的价格部分按原价的七折出售.某顾客打算在促销期间到这两家商场中的一家去购物,设该顾客在一次购物中的购物金额的原价为x元,让利后的购物金额为y元(1)、分别就甲乙两家商场写出y与x的函数关系式.(2)、该顾客应如何选择这两家商场去购物会更省钱?并说明理由.23. 如图, 正方形 的边 在正方形 的边 上, 、 、 点在一条点线上, 且正方形 与正方形 的边长分别为 和 ,在 上截取 .连接 、 .
(1)、求线段 的长(2)、试判断直线 与 的位置关系,并说明理由22. 甲乙两家商场以同样价格销售相同的商品,在同一促销期间两家商场都让利酬宾.甲商场所有商品都按原价的八折出售,乙商场只对一次购物中超过100元后的价格部分按原价的七折出售.某顾客打算在促销期间到这两家商场中的一家去购物,设该顾客在一次购物中的购物金额的原价为x元,让利后的购物金额为y元(1)、分别就甲乙两家商场写出y与x的函数关系式.(2)、该顾客应如何选择这两家商场去购物会更省钱?并说明理由.23. 如图, 正方形 的边 在正方形 的边 上, 、 、 点在一条点线上, 且正方形 与正方形 的边长分别为 和 ,在 上截取 .连接 、 .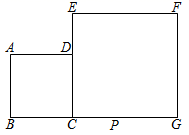 (1)、先补全图形,猜想 与 之间的大小关系,并说明理由(2)、图中是否存在通过旋转、平移、翻折等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说出理由(3)、若把这个图形滑 、 的成块,请你把它们拼成个大正方形,在原图上画出示意图,并求出这个大正方形的面积.
(1)、先补全图形,猜想 与 之间的大小关系,并说明理由(2)、图中是否存在通过旋转、平移、翻折等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说出理由(3)、若把这个图形滑 、 的成块,请你把它们拼成个大正方形,在原图上画出示意图,并求出这个大正方形的面积.