河南省商丘市永城市2019-2020学年八年级下学期数学期末考试试卷(B)
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
1. 二次根式 有意义的x的取值范围是( )A、 B、 C、 D、2. 已知 中, ,则 的度数为( )A、125° B、135° C、145° D、155°3. 已知三角形的三边长a,b,c满足 ,则该三角形的形状为( )A、等腰三角形 B、锐角三角形 C、钝角三角形 D、直角三角形4. 菱形具有而矩形不具有的性质是( )A、两组对边分别平行 B、对角线互相垂直 C、对角线互相平分 D、两组对角分别相等5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,直线 和直线 交于点 ,根据图象分析,关于x的方程 的解为( )
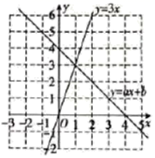 A、 B、 C、 D、7. 如图所示:数轴上点A所表示的数为a,则a的值是( )
A、 B、 C、 D、7. 如图所示:数轴上点A所表示的数为a,则a的值是( )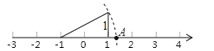 A、+1 B、-1 C、-+1 D、--18. 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,并分别按 的比例计入总评成绩,小明的三项成绩分别是 , , (单位:分)他的总评成绩是( )A、 分 B、 分 C、 分 D、 分9. 已知一次函数 的图象如图所示,则 的图象可能是( )
A、+1 B、-1 C、-+1 D、--18. 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,并分别按 的比例计入总评成绩,小明的三项成绩分别是 , , (单位:分)他的总评成绩是( )A、 分 B、 分 C、 分 D、 分9. 已知一次函数 的图象如图所示,则 的图象可能是( )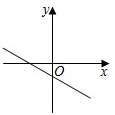 A、
A、 B、
B、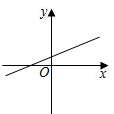 C、
C、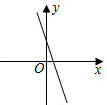 D、
D、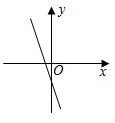 10. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
10. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )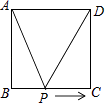 A、
A、 B、
B、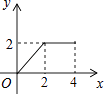 C、
C、 D、
D、
二、填空题
-
11. 若 与最简二次根式 可以合并,则实数a的值是.12. 将直线 向上平移3个单位长度,所得直线的解析式为.13. 据4月13日新华社报道,我国由陈薇院士组织的腺病毒载体重组新冠病毒疫苗率先进入第二期临床试验.我们从中选取甲、乙、丙三组各有7名志愿者,测得三组志愿者的体重数据的平均数都是58,方差分别为S甲2=36,S乙2=25,S丙2=16,则数据波动最小的一组是.14. 在菱形 中,对角线 、 交于点 ,点 为 中点,过点 作 于点 交 于点 ,连接 ,若 则 °.
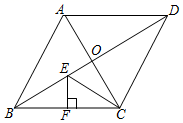 15. 在平面直角坐标系 中,已知一次函数 的图象过点 ,与x轴交于点A,与y轴交于点B,且 ,那么点A的坐标是.
15. 在平面直角坐标系 中,已知一次函数 的图象过点 ,与x轴交于点A,与y轴交于点B,且 ,那么点A的坐标是.三、解答题
-
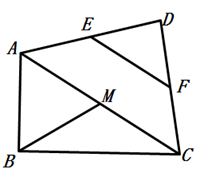
16.(1)、计算:(2)、计算:17. 如图,在四边形 中, ,接 ,E,F,M分别是 , , 的中点,连接 , .求证: .
 18. 已知一次函数 的图象经过 , 两点.(1)、求k、b的值;(2)、若一次函数 的图象与x轴的交点坐标为 ,求a的值.19. 如图,在平面直角坐标系中,正方形网格的每个小方格都是边长为1的小正方形, 的顶点都在格点上.
18. 已知一次函数 的图象经过 , 两点.(1)、求k、b的值;(2)、若一次函数 的图象与x轴的交点坐标为 ,求a的值.19. 如图,在平面直角坐标系中,正方形网格的每个小方格都是边长为1的小正方形, 的顶点都在格点上. (1)、试判断 的形状,并说明理由;(2)、求 的面积.20. 如图,在四边形 中, , 相交于点O,O是 的中点, .
(1)、试判断 的形状,并说明理由;(2)、求 的面积.20. 如图,在四边形 中, , 相交于点O,O是 的中点, .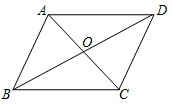 (1)、求证:四边形 是平行四边形.(2)、若 ,且 ,则 的周长为.21. 某校九年级学生积极响应“停课不停学”,通过网课等方式学习了解防疫防控知识.为了解该校九年级学生的防疫知识学习情况,网上随机抽查了40名同学的防疫知识问卷调查(满分10分).根据答卷统计,获取的样本数据,制作出了如下的条形统计图和扇形统计图.据相关信息,解答下列问题:
(1)、求证:四边形 是平行四边形.(2)、若 ,且 ,则 的周长为.21. 某校九年级学生积极响应“停课不停学”,通过网课等方式学习了解防疫防控知识.为了解该校九年级学生的防疫知识学习情况,网上随机抽查了40名同学的防疫知识问卷调查(满分10分).根据答卷统计,获取的样本数据,制作出了如下的条形统计图和扇形统计图.据相关信息,解答下列问题: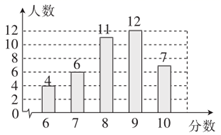
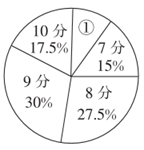 (1)、扇形①的圆心角的度数是;(2)、求40个样本数据的平均数、众数、中位数;(3)、若该校九年级共有320名学生,估计该校九年级防疫知识问卷调查得满分学生的人数.22. 某商场销售10台A型和20台B型加湿器的利润为2500元,销售20台A型和10台B型加湿器的利润为2000元.(1)、求每台A型加湿器和每台B型加湿器的销售利润;(2)、该商场计划一次购进两种型号的加湿器共100台,设购进A型加湿器 台,这100台加湿器的销售总利润为y元.
(1)、扇形①的圆心角的度数是;(2)、求40个样本数据的平均数、众数、中位数;(3)、若该校九年级共有320名学生,估计该校九年级防疫知识问卷调查得满分学生的人数.22. 某商场销售10台A型和20台B型加湿器的利润为2500元,销售20台A型和10台B型加湿器的利润为2000元.(1)、求每台A型加湿器和每台B型加湿器的销售利润;(2)、该商场计划一次购进两种型号的加湿器共100台,设购进A型加湿器 台,这100台加湿器的销售总利润为y元.①求y关于x的函数关系式;
②若B型加湿器的进货量不超过A型加湿器的2倍,则该商场应怎样进货才能使销售总利润最大?
23. 如图,矩形 的两条边 、 分别在y轴和x轴上,已知点B 坐标为(4,–3).把矩形 沿直线 折叠,使点C落在点A处,直线 与 、 、 的交点分别为D、F、E.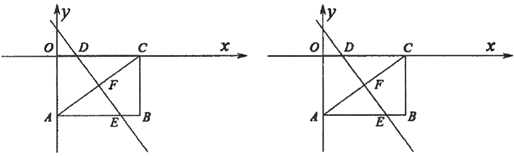 (1)、线段 ;(2)、求点D坐标及折痕 的长;(3)、若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请求出点Q的坐标;若不存在,请说明理由;
(1)、线段 ;(2)、求点D坐标及折痕 的长;(3)、若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请求出点Q的坐标;若不存在,请说明理由;