广西壮族自治区柳州市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、选择题
-
1. 若 在实数范围内有意义,则x的取值范围( )A、x≥2 B、x≤2 C、x>2 D、x<22. 如图,分别以直角 三边为边向外作三个正方形,其面积分别用 表示,若 , ,那么 ( )
 A、9 B、5 C、53 D、453. 甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,下列说法正确的是( )A、乙的成绩比较稳定 B、甲的成绩比较稳定 C、乙射中的总环数比甲多 D、甲射中的总环数比乙多4. 若函数 是一次函数,则k的值是( )A、1 B、2 C、3 D、45. 下列计算正确的是( )A、 B、 C、 D、6. 关于直线y=4x,下列说法正确的是( )A、直线过原点 B、y随x的增大而减小 C、直线经过点(1,2) D、直线经过二、四象限7. 某次歌唱比赛中,由10个评委分别对甲、乙两名选手打分,按照规则去掉一个最高分和一个最低分,请问去掉分数后,下列统计量一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,菱形 中,对角线 交于点O,若 , ,则菱形 的面积是( )
A、9 B、5 C、53 D、453. 甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙的平均数均是7,甲的方差是1.2,乙的方差是5.8,下列说法正确的是( )A、乙的成绩比较稳定 B、甲的成绩比较稳定 C、乙射中的总环数比甲多 D、甲射中的总环数比乙多4. 若函数 是一次函数,则k的值是( )A、1 B、2 C、3 D、45. 下列计算正确的是( )A、 B、 C、 D、6. 关于直线y=4x,下列说法正确的是( )A、直线过原点 B、y随x的增大而减小 C、直线经过点(1,2) D、直线经过二、四象限7. 某次歌唱比赛中,由10个评委分别对甲、乙两名选手打分,按照规则去掉一个最高分和一个最低分,请问去掉分数后,下列统计量一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,菱形 中,对角线 交于点O,若 , ,则菱形 的面积是( )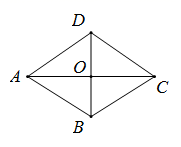 A、12 B、24 C、10 D、489. 已知一次函数 的图象如图所示,则一次函数 的图象可能是下列选项中的( )
A、12 B、24 C、10 D、489. 已知一次函数 的图象如图所示,则一次函数 的图象可能是下列选项中的( )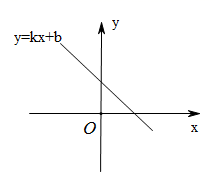 A、
A、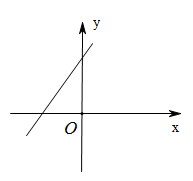 B、
B、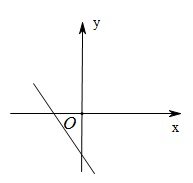 C、
C、 D、
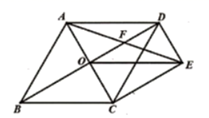
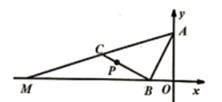
D、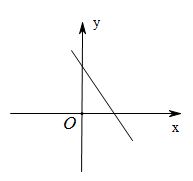 10. 如图,点 , 是正方形 的两个顶点,以对角线 为边作正方形 ,再以正方形 的对角线 为边作正方形 , ,依此规律,则点 的坐标是( )
10. 如图,点 , 是正方形 的两个顶点,以对角线 为边作正方形 ,再以正方形 的对角线 为边作正方形 , ,依此规律,则点 的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 比较大小:12. “两直线平行,内错角相等”的逆命题是 .13. 的三边分别是6,8,10,则这个三角形的最大内角的度数是.14. 中, , ,则 的周长为.15. 某公司招聘职员,对甲、乙两位候选人进行了形体、口才、专业水平的考察,他们的成绩(十分制)如下表:
形体
口才
专业水平
甲
8
8
9
乙
8
9
7
若公司将形体、口才、专业水平按照3:2:5的比例计算甲、乙两人的平均成绩,则将被录取.
16. 如图,在正方形 中,对角线 与 相交于点 , 为 上一点, , 为 的中点.若 的周长为18,则 的长为 .
三、解答题
-
17. 计算:18. 某天下午,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与离家距离的关系示意图,小刚在每个时间段内均是匀速骑行,根据图中提供的信息回答下列问题:
 (1)、小刚家到学校的路程是米,小刚在书店停留了分钟;(2)、若骑单车的速度超过300米/分就超过了安全限度,请判断小刚骑车的最快速度是否在安全限度内?并说明理由.19. 如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.求证:四边形AECF是平行四边形.
(1)、小刚家到学校的路程是米,小刚在书店停留了分钟;(2)、若骑单车的速度超过300米/分就超过了安全限度,请判断小刚骑车的最快速度是否在安全限度内?并说明理由.19. 如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.求证:四边形AECF是平行四边形.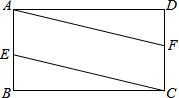 20. 当今,青少年视力水平下降已引起全社会的关注,为了了解某市30000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如下,解答下列问题:
20. 当今,青少年视力水平下降已引起全社会的关注,为了了解某市30000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如下,解答下列问题: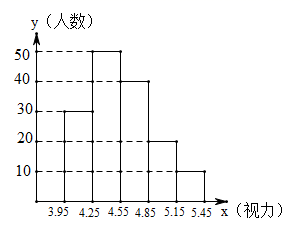 (1)、本次调查共抽取了名学生;(2)、若视力为4.85及以上为正常,试估计该市学生的视力正常的人数约为多少?(3)、请你根据调查结果提一条合理化建议.21. 已知一次函数 ,当 时, .(1)、求一次函数的解析式;(2)、将该函数的图象向上平移6个单位长度,求平移后的图象与x轴交点的坐标;(3)、在(2)的条件下,直接写出 时,x的取值范围.
(1)、本次调查共抽取了名学生;(2)、若视力为4.85及以上为正常,试估计该市学生的视力正常的人数约为多少?(3)、请你根据调查结果提一条合理化建议.21. 已知一次函数 ,当 时, .(1)、求一次函数的解析式;(2)、将该函数的图象向上平移6个单位长度,求平移后的图象与x轴交点的坐标;(3)、在(2)的条件下,直接写出 时,x的取值范围.