云南省大理州巍山县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-27 类型:期末考试
一、填空题
-
1. 若式子 有意义,则x的取值范围是.
-
2. 一次函数y=2x-6的图象与x轴的交点坐标为.
-
3. 在平面直角坐标系中,点A、B、C的坐标分别是 , , ,若以点A、B、C、D为顶点的四边形是平行四边形,则满足条件的D点共有个.
-
4. 如表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差:
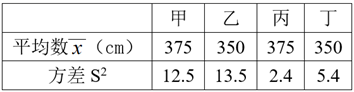
根据表中数据,要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛,应该选择.
-
5. 四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC为度.
-
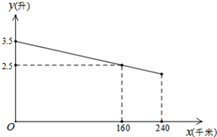
6. 李老师开车从甲地到相距240km的乙地,如果油箱剩余油量 与行驶里程 之间是一次函数关系,其图象如图所示,那么,达到乙地时油箱剩余油量是L.
二、选择题
-
7. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、
-
8. 以下列各数为边长,能构成直角三角形的是( )A、1,2,2 B、1, ,2 C、4,5,6 D、1,1,
-
9. 下列计算正确的是( )A、 × =4 B、 + = C、 ÷ =2 D、 =﹣15
-
10. 矩形具有而菱形不具有的性质是( )
A、两组对边分别平行 B、对角线相等 C、对角线互相平分 D、两组对角分别相等 -
11. 一次函数y=﹣5x+3的图象不经过第( )象限A、一 B、二 C、三 D、四
-
12. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
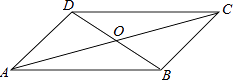 A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC -
13. 如图,函数 和 的图象相交于A(m,3),则不等式 的解集为( )
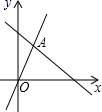 A、 B、 C、 D、
A、 B、 C、 D、 -
14. 正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是( )
 A、(2n﹣1,2n﹣1) B、(2n﹣1+1,2n﹣1) C、(2n﹣1,2n﹣1) D、(2n﹣1,n)
A、(2n﹣1,2n﹣1) B、(2n﹣1+1,2n﹣1) C、(2n﹣1,2n﹣1) D、(2n﹣1,n)
三、解答题
-
15. 计算:(1)、(2)、
-
16. 化简求值: ÷ • ,其中x= -2
-
17. 如图,点E,F为▱ABCD的对角线BD上的两点,连接AE,CF,∠AEB=∠CFD.求证:AE=CF.
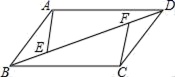
-
18. 如图,在四边形 中, , , , .
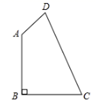
求 的度数.
-
19. 直线 经过点 、
 (1)、求直线 的解析式;(2)、若点C在x轴上,且 求出点C坐标.
(1)、求直线 的解析式;(2)、若点C在x轴上,且 求出点C坐标. -
20. 为了普及环保知识,增强环保意识,某中学组织了全校环保知识竞赛活动,初中各年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
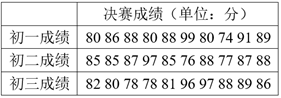 (1)、请你填写下表中的a= , b= , c=;
(1)、请你填写下表中的a= , b= , c=;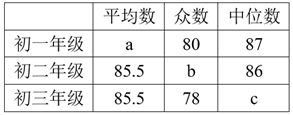 (2)、从以下两个不同的角度对三个年级的决赛成绩进行分析:
(2)、从以下两个不同的角度对三个年级的决赛成绩进行分析:①从众数和平均数相结合看(分析哪个年级成绩好些);
②从平均数和中位数相结合看(分析哪个年级成绩好些).
(3)、如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强些?并说明理由. -
21.
如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E.
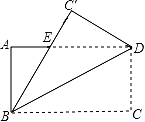 (1)、判断△EBD的形状,并说明理由;(2)、求DE的长.
(1)、判断△EBD的形状,并说明理由;(2)、求DE的长. -
22. 如图是小阳同学所走的路程s(米)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题:
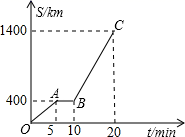 (1)、小阳同学在前5分钟内的平均速度是多少?(2)、小阳同学在中途停了多长时间?(3)、当10≤t≤20时,求s与t的函数关系式.
(1)、小阳同学在前5分钟内的平均速度是多少?(2)、小阳同学在中途停了多长时间?(3)、当10≤t≤20时,求s与t的函数关系式. -
23. 在抗击新冠肺炎的非常时期,某医药器械厂接受了生产一批高质量医用口罩的任务,要求在8天之内(含8天)生产A型和B型两种型号的口罩共5万只,其中A型口罩不得少于1.8万只,该厂的生产能力是:若生产A型口罩每天能生产0.6万只,若生产B型口罩每天能生产0.8万只,已知生产一只A型口罩可获利0.5元,生产一只B型口罩可获利0.3元.若设该厂在这次任务中生产了A型口罩x万只.(1)、该厂生产A型口罩可获利润万元,生产B型口罩可获利润万元.(2)、设该厂这次生产口罩的总利润是y万元,试写出y关于x的函数关系式,并求出自变量x的取值范围;(3)、在完成任务的前提下,如何安排生产A型和B型口罩的只数,使获得的总利润最大,最大利润是多少?(4)、若要在最短时间内完成任务,如何来安排生产A型和B型口罩的只数?最短时间是几天?
