江西省南昌市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,有 、 两点,则A与B关于( )A、x轴对称 B、y轴对称 C、原点对称 D、直线 对称3. 在 中,若 ,则 的补角的度数是( )A、36° B、72° C、108° D、144°4. 如图,若 ,则下列结论错误的是( )
2. 在平面直角坐标系中,有 、 两点,则A与B关于( )A、x轴对称 B、y轴对称 C、原点对称 D、直线 对称3. 在 中,若 ,则 的补角的度数是( )A、36° B、72° C、108° D、144°4. 如图,若 ,则下列结论错误的是( )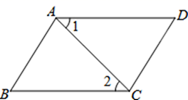 A、 B、 C、 D、5. 有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长( )A、最小值是11 B、最小值是12 C、最大值是14 D、最大值是156. 如图, ,点P在边 上, ,点M、N在边 上, ,若 ,则 是( )
A、 B、 C、 D、5. 有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长( )A、最小值是11 B、最小值是12 C、最大值是14 D、最大值是156. 如图, ,点P在边 上, ,点M、N在边 上, ,若 ,则 是( )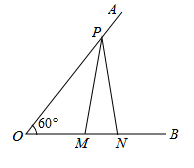 A、3 B、4 C、5 D、67. 把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )
A、3 B、4 C、5 D、67. 把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )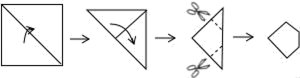 A、六边形 B、八边形 C、十二边形 D、十六边形8. 如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
A、六边形 B、八边形 C、十二边形 D、十六边形8. 如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( ) A、90°- α B、90°+ α C、 D、360°-α
A、90°- α B、90°+ α C、 D、360°-α二、填空题
-
9. △ABC中,∠A=50°,∠B=60°,则∠C=度.10. 如图,若正五边形和正六边形有一边重合,则∠BAC=.
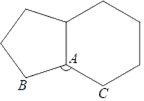 11. 若等腰三角形的顶角为 ,则这个等腰三角形的底角的度数 .12. 如图,若 于点B, 于点E, , , , ,则 的度数是.
11. 若等腰三角形的顶角为 ,则这个等腰三角形的底角的度数 .12. 如图,若 于点B, 于点E, , , , ,则 的度数是.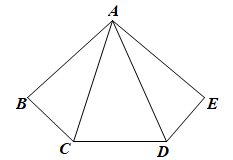 13. 如图,在平面直角坐标系中,点A(−2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是 .
13. 如图,在平面直角坐标系中,点A(−2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是 .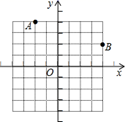 14. 当三角形中一个内角 是另一个内角 的2倍时,则称此三角形为“倍角三角形”,其中角 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是.
14. 当三角形中一个内角 是另一个内角 的2倍时,则称此三角形为“倍角三角形”,其中角 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是.三、解答题
-
15. 如图, , .
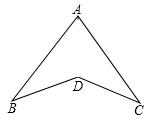 (1)、求证: ;(2)、若 ,求证: .16. 已知三角形的两边长为4和6,第三条边长x最小.(1)、求x的取值范围;(2)、当x为何值时,组成的三角形周长最大?最大值是多少?17. 如图,在棋盘中有 、 、 三个棋子,若再添加一个棋子P,使A、O、B、P四个棋子成为一个轴对称图形,请在三个图中分别画出三种不同的对称轴,并分别写出棋子P的坐标.
(1)、求证: ;(2)、若 ,求证: .16. 已知三角形的两边长为4和6,第三条边长x最小.(1)、求x的取值范围;(2)、当x为何值时,组成的三角形周长最大?最大值是多少?17. 如图,在棋盘中有 、 、 三个棋子,若再添加一个棋子P,使A、O、B、P四个棋子成为一个轴对称图形,请在三个图中分别画出三种不同的对称轴,并分别写出棋子P的坐标.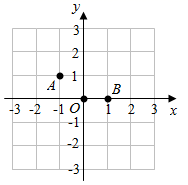
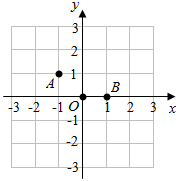
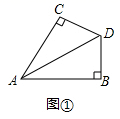
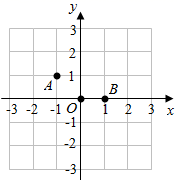 18. 如图,已知 平分 ,且 .
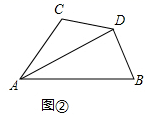
18. 如图,已知 平分 ,且 .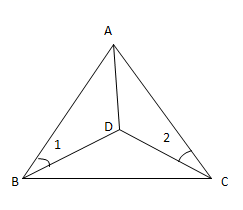 (1)、求证: ;(2)、判断 与 的位置关系,并说明理由.19. 如图1,已知线段 、 相交于点O,连接 、 .
(1)、求证: ;(2)、判断 与 的位置关系,并说明理由.19. 如图1,已知线段 、 相交于点O,连接 、 .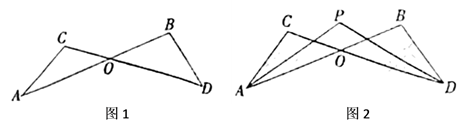 (1)、求证: ;(2)、如图2, 与 的平分线 、 相交于点P,求证: .20. 在△ABC中,AB=AC , 点D在边BC上,点E在边AC上,且AD=AE .
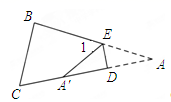
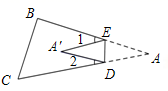
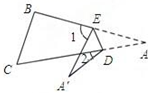
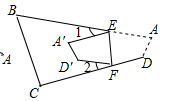
(1)、求证: ;(2)、如图2, 与 的平分线 、 相交于点P,求证: .20. 在△ABC中,AB=AC , 点D在边BC上,点E在边AC上,且AD=AE .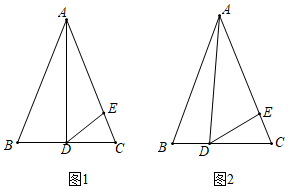 (1)、如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;(2)、如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
(1)、如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;(2)、如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.