江西省赣州市宁都县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 下列图形中,只有两条对称轴的图形是( ).A、
 B、
B、 C、
C、 D、
D、 2. 根据下列条件判断,以a,b,c为边的三角形不是直角三角形的是( )A、 , , B、 , , C、 , , D、a:b: :12:133. 估计20的算术平方根的大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间4. 用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC , 需要证明△D′O′C′≌△DOC , 则这两个三角形全等的依据是( )
2. 根据下列条件判断,以a,b,c为边的三角形不是直角三角形的是( )A、 , , B、 , , C、 , , D、a:b: :12:133. 估计20的算术平方根的大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间4. 用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC , 需要证明△D′O′C′≌△DOC , 则这两个三角形全等的依据是( ) A、SAS B、SSS C、ASA D、AAS5. 等腰三角形一腰上的高与另一腰的夹角为 ,则顶角的度数为( )A、 B、 或 C、 或 D、 或6. 如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A、SAS B、SSS C、ASA D、AAS5. 等腰三角形一腰上的高与另一腰的夹角为 ,则顶角的度数为( )A、 B、 或 C、 或 D、 或6. 如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )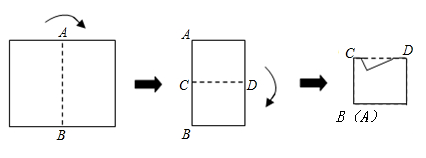 A、
A、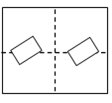 B、
B、 C、
C、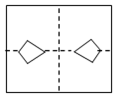 D、
D、
二、填空题
-
7. 若一扇窗户打开后,用窗钩将其固定,主要运用的几何原理是 .8. 三角形两边长分别是3、5,第三边长为偶数,则第三边长为9. 如图,甲、乙两岸之间要架一座桥梁,从甲岸测得桥梁的走向是北偏东50°,如果甲、乙两岸同时开工.要使桥梁准确连接,那么在乙岸施工时,应按β为度的方向动工.
 10. 如图,已知线段AB、CD相交于点O , 且∠A=∠B , 若有△AOC≌△BOD , 需补充一个条件是 .
10. 如图,已知线段AB、CD相交于点O , 且∠A=∠B , 若有△AOC≌△BOD , 需补充一个条件是 . 11. 如图, 是 斜边 上的高,将 沿 折叠,点 恰好落在 边的中点 处,则 等于 .
11. 如图, 是 斜边 上的高,将 沿 折叠,点 恰好落在 边的中点 处,则 等于 . 12. 已知有两个三角形全等,若一个三角形三边的长分别为3、5、7,另一个三角形三边的长分别为3、3a﹣2b、a+2b , 则a+b= .
12. 已知有两个三角形全等,若一个三角形三边的长分别为3、5、7,另一个三角形三边的长分别为3、3a﹣2b、a+2b , 则a+b= .三、解答题
-
13. 计算(1)、(2)、14. 实数a、b在数轴上的位置如图所示,请化简:|a|﹣ ﹣ .
 15. 一个多边形的内角和比它外角和的3倍少180°,求这个多边形的边数.16.
15. 一个多边形的内角和比它外角和的3倍少180°,求这个多边形的边数.16.△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
 (1)、作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标(2)、作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.17. 如图,AM=AN , 点B和点C分别为∠MAN两边上的点,AB=AC . 按下列语句画出图形:(要求用无刻度直尺作图,)
(1)、作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标(2)、作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.17. 如图,AM=AN , 点B和点C分别为∠MAN两边上的点,AB=AC . 按下列语句画出图形:(要求用无刻度直尺作图,) (1)、AD⊥BC , 垂足为D;(2)、在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:18. 如图.在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE , BE=CF , AB∥ED . 求证:AC=DF .
(1)、AD⊥BC , 垂足为D;(2)、在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:18. 如图.在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE , BE=CF , AB∥ED . 求证:AC=DF . 19. 如图梯形ABCD中,AD∥BC , AB=AD=CD , BD⊥CD , 求∠C的度数.
19. 如图梯形ABCD中,AD∥BC , AB=AD=CD , BD⊥CD , 求∠C的度数. 20. 如图,点E在△ABC外部,点D在边BC上,DE交AC于点F.若∠1=∠2=∠3,AC=AE,求证△ABC≌△ADE.
20. 如图,点E在△ABC外部,点D在边BC上,DE交AC于点F.若∠1=∠2=∠3,AC=AE,求证△ABC≌△ADE.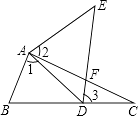 21. 如图,已知AC平分∠BAD , CE⊥AB于E , CF⊥AD于F , 且BC=CD ,
21. 如图,已知AC平分∠BAD , CE⊥AB于E , CF⊥AD于F , 且BC=CD , (1)、求证:△BCE≌△DCF;(2)、若AB=21,AD=9,BC=CD=10,求BE的长.22. 如图,长方形ABCD中AD∥BC , 边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处.
(1)、求证:△BCE≌△DCF;(2)、若AB=21,AD=9,BC=CD=10,求BE的长.22. 如图,长方形ABCD中AD∥BC , 边AB=4,BC=8.将此长方形沿EF折叠,使点D与点B重合,点C落在点G处. (1)、试判断△BEF的形状,并说明理由;(2)、若AE=3,求△BEF的面积.23. 数学课上,李老师出示了如下的题目:
(1)、试判断△BEF的形状,并说明理由;(2)、若AE=3,求△BEF的面积.23. 数学课上,李老师出示了如下的题目:“在等边三角形ABC中,点E在AB上,点D在CB的延长
线上,且ED=EC,如图,试确定线段AE与DB的大小关系,
并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
 (1)、特殊情况,探索结论
(1)、特殊情况,探索结论当点 为 的中点时,如图1,确定线段 与 的大小关系,请你直接写出结论: (填“>”,“<”或“=”).
 (2)、特例启发,解答题目
(2)、特例启发,解答题目解:题目中, 与 的大小关系是: (填“>”,“<”或“=”).理由如下:
如图2,过点 作 ,交 于点 .(请你完成以下解答过程)
 (3)、拓展结论,设计新题
(3)、拓展结论,设计新题在等边三角形 中,点 在直线 上,点 在直线 上,且 .若 的边长为1, ,求 的长(请你直接写出结果).