江西省抚州市乐安县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-27 类型:期中考试
一、单选题
-
1. 在3.14, , ,π, ,0.1010010001…中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 若 ,则a的相反数是( )A、6 B、-6 C、36 D、-363. 已知点P1(a+1,4)和P2(2,b)关于y轴对称,则a﹣b的值为( )A、﹣7 B、﹣1 C、1 D、54. 三角形的三边长a,b,c满足关系式(a+2b﹣60)2+|b﹣18|+ =0,则这个三角形是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形5. 点 到原点的距离为( )A、3 B、4 C、5 D、以上都不对6. 若直线y=﹣x+a与直线y=x+b的交点坐标为(2,8),则a﹣b的值为( )
A、2 B、4 C、6 D、8二、填空题
-
7. 写出一个比2大比3小的无理数(用含根号的式子表示) .
8. 若 ,则 的立方根是.9. 如图,数轴上点 , 对应的实数分别为1, ,点 关于点 的对称点为点 ,则点 所表示的实数是.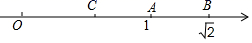 10. 在平面直角坐标系中,点A(-1,x2+1)一定在第象限.11. 如果电影票上的“5排2号”记作(5,2),那么(4,3)表示.12. 已知 ,则a的值为.13. 若 的整数部分为 ,小数部分为 ,则 的值是.
10. 在平面直角坐标系中,点A(-1,x2+1)一定在第象限.11. 如果电影票上的“5排2号”记作(5,2),那么(4,3)表示.12. 已知 ,则a的值为.13. 若 的整数部分为 ,小数部分为 ,则 的值是.三、解答题
-
14.(1)、已知 , , 是9的算术平方根,求 的平方根;(2)、求图中阴影部分的面积.
 15. 计算(1)、( )2﹣( ﹣ )( )(2)、( )﹣( ﹣ )16. 在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,1),B(0,2),C(-1,n),试求n的值.17. 在如图所示的平面直角坐标系中:
15. 计算(1)、( )2﹣( ﹣ )( )(2)、( )﹣( ﹣ )16. 在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,1),B(0,2),C(-1,n),试求n的值.17. 在如图所示的平面直角坐标系中: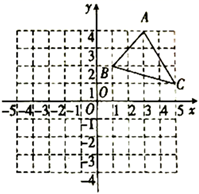 (1)、画出三角形 关于 轴成轴对称图形的三角形 ;(2)、写出(1)中 , , 的坐标.18. 已知,如图所示的一块地,已知AD=12米,CD=9米,∠ADC=90°,AB=39米,BC=36米,求这块地的面积.
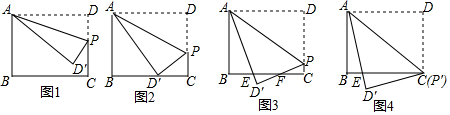
(1)、画出三角形 关于 轴成轴对称图形的三角形 ;(2)、写出(1)中 , , 的坐标.18. 已知,如图所示的一块地,已知AD=12米,CD=9米,∠ADC=90°,AB=39米,BC=36米,求这块地的面积.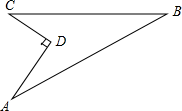 19. 在平面直角坐标系中,已知点 , .(1)、若点 在 轴上,求点 的坐标;(2)、若 轴,求 的值.20. 如图,在长方形 中,边 , ,以点 为原点, , 所在的直线为 轴和 轴,建立直角坐标系.
19. 在平面直角坐标系中,已知点 , .(1)、若点 在 轴上,求点 的坐标;(2)、若 轴,求 的值.20. 如图,在长方形 中,边 , ,以点 为原点, , 所在的直线为 轴和 轴,建立直角坐标系.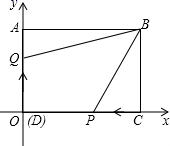 (1)、点 的坐标为 ,则 点坐标为 , 点坐标为;(2)、当点 从 出发,以2单位/秒的速度沿 方向移动(不过 点), 从原点 出发以1单位/秒的速度沿 方向移动(不过 点), , 同时出发,在移动过程中,四边形 的面积是否变化?若不变,求其值;若变化,求其变化范围.21. 如图,一根长 米的木棒( ),斜靠在与地面( )垂直的墙( )上,且木棒顶端与地面的距离( )为9米,当木棒 端沿墙下滑至点 时, 端沿地面向右滑行至点 .
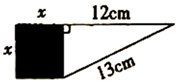
(1)、点 的坐标为 ,则 点坐标为 , 点坐标为;(2)、当点 从 出发,以2单位/秒的速度沿 方向移动(不过 点), 从原点 出发以1单位/秒的速度沿 方向移动(不过 点), , 同时出发,在移动过程中,四边形 的面积是否变化?若不变,求其值;若变化,求其变化范围.21. 如图,一根长 米的木棒( ),斜靠在与地面( )垂直的墙( )上,且木棒顶端与地面的距离( )为9米,当木棒 端沿墙下滑至点 时, 端沿地面向右滑行至点 .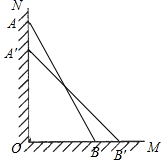 (1)、求 的长;(2)、当 米时,求 的长(结果保留根号).
(1)、求 的长;(2)、当 米时,求 的长(结果保留根号).