初中数学浙教版七年级上册第五章 一元一次方程 单元检测(提高篇)
试卷更新日期:2020-09-26 类型:单元试卷
一、单选题
-
1. 若方程(a+4)x|a|-3+2=6是关于x的一元一次方程,则a的值为( )A、-4 B、4 C、-3 D、32. 下列各对等式,是根据等式的性质进行变形的,其中错误的是( ).A、4x-1=5x+2→x=-3 B、 C、 D、3. 在有理数范围内定义运算“*”,其规则为a*b= ,则方程(2*3)(4*x)=49的解为( )A、﹣3 B、﹣55 C、﹣56 D、554. 一个两位数,个位上的数字与十位上的数字之和为7,如果这个两位数加上45则恰好成为个位数字与十位数字对调后组成的新两位数,则原来的两位数是( )A、61 B、52 C、16 D、255. 中国古代数学著作《算法统宗》中有这样一段记载,“三百七十八里关;初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是;有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到关口,则此人第一和第六这两天共走了( )A、102里 B、126里 C、192里 D、198里6. 把 这 个数填入 方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图 ),是世界上最早的“幻方”.图 是仅可以看到部分数值的“九宫格”,则其中 的值为( )
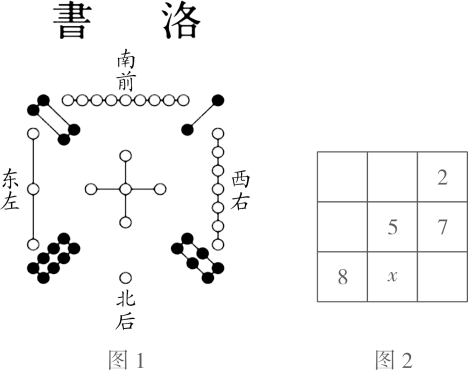 A、1 B、3 C、4 D、67. 如果甲、乙、丙三个村合修一段水渠,计划出工65人,按各村受益土地面积3:4:6出工,求各村应出工的人数. ①设甲、乙、丙三村分别派3x,4x,6x人,依题意可得3x+4x+6x=65; ②设甲村派x人,依题意得x+4x+6x=65; ③设甲村派x人,依题意得x+x+2x=65; ④设丙村派x人,依题意得3x+4x+x=65.上面所列方程中正确的是( )A、①② B、②③ C、③④ D、①③8. 一列数,按一定规律排列:-1,3,-9.27,-81,…,从中取出三个相邻的数,若三个数的和为a,则这三个数中最大的数与最小的数的差为( )A、
A、1 B、3 C、4 D、67. 如果甲、乙、丙三个村合修一段水渠,计划出工65人,按各村受益土地面积3:4:6出工,求各村应出工的人数. ①设甲、乙、丙三村分别派3x,4x,6x人,依题意可得3x+4x+6x=65; ②设甲村派x人,依题意得x+4x+6x=65; ③设甲村派x人,依题意得x+x+2x=65; ④设丙村派x人,依题意得3x+4x+x=65.上面所列方程中正确的是( )A、①② B、②③ C、③④ D、①③8. 一列数,按一定规律排列:-1,3,-9.27,-81,…,从中取出三个相邻的数,若三个数的和为a,则这三个数中最大的数与最小的数的差为( )A、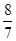 a
B、
a
B、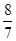 |a|
C、
|a|
C、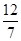 |a|
D、
|a|
D、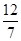 a
9. 将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2 . 已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )
a
9. 将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2 . 已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是( )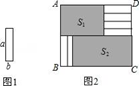 A、 b= a B、 b= C、 b=
A、 b= a B、 b= C、 b=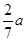 D、 b=
D、 b= 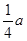 10. 已知一个由50个偶数排成的数阵.用如图所示的框去框住四个数,并求出这四个数的和.在下列给出备选答案中,有可能是这四个数的和的是( )
10. 已知一个由50个偶数排成的数阵.用如图所示的框去框住四个数,并求出这四个数的和.在下列给出备选答案中,有可能是这四个数的和的是( )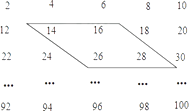 A、80 B、148 C、172 D、220
A、80 B、148 C、172 D、220二、填空题
-
11. 已知关于x的一元一次方程 +5=2019x+m的解为x=2018,那么关于y的一元一次方程 ﹣5=2019(5﹣y)﹣m的解为.12. 现定义一种新运算,对于任意有理数a、b、c、d满足 =ad﹣bc,若对于含未知数x的式子满足 =3,则未知数x= .13. 已知关于
 的一元一次方程 x+3=2x+b的解为 ,那么关于 的一元一次方程 (y+1)+3=2(y+1)+b的解为 . 14. 一般情况下, 不成立,但是,有些数可以使它成立,例如,m=n=0,我们称使得 成立的一对数m、n为“相伴数对”,记作(m,n),如果(m,3)是“相伴数对”那么m的值是;小明发现(x,y)是“相伴数对”,则式子 的值是.15. 把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长比宽多 )的盒底上,底面为被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为 ,图③中阴影部分的周长为 ,则 .
的一元一次方程 x+3=2x+b的解为 ,那么关于 的一元一次方程 (y+1)+3=2(y+1)+b的解为 . 14. 一般情况下, 不成立,但是,有些数可以使它成立,例如,m=n=0,我们称使得 成立的一对数m、n为“相伴数对”,记作(m,n),如果(m,3)是“相伴数对”那么m的值是;小明发现(x,y)是“相伴数对”,则式子 的值是.15. 把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长比宽多 )的盒底上,底面为被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为 ,图③中阴影部分的周长为 ,则 .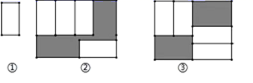 16. 2019年4月4日,中国国际女足锦标赛半决赛在武汉进行,这场由中国队迎战俄罗斯队的比赛牵动着众多足球爱好者的心.在未开始检票入场前,已有1200名足球爱好者排队等待入场.假设检票开始后,每分钟赶来的足球爱好者人数是固定的,1个检票口每分钟可以进入40人.如果4个检票口同时检票,15分钟后排队现象消失;如果7个检票口同时检票,分钟后排队现象消失.
16. 2019年4月4日,中国国际女足锦标赛半决赛在武汉进行,这场由中国队迎战俄罗斯队的比赛牵动着众多足球爱好者的心.在未开始检票入场前,已有1200名足球爱好者排队等待入场.假设检票开始后,每分钟赶来的足球爱好者人数是固定的,1个检票口每分钟可以进入40人.如果4个检票口同时检票,15分钟后排队现象消失;如果7个检票口同时检票,分钟后排队现象消失.三、解答题
-
17. 解方程,(1)、(2)、18. 小明解方程 时,由于粗心大意,在去分母时,方程左边的1没有乘以10,由此求得的解为x=4,试求a的值,并正确地求出方程的解.
19. 小明每天早上要在7:50之前赶到距家900米的学校上学.小明以60米/分的速度出发10分后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以160米/分的速度去追小明,爸爸能否在小明进学校前追上他?若能,请说明理由,若不能,请计算,爸爸的速度至少为多少时才能赶在小明进学校前追上他?20. 能否从等式(2a﹣1)x=3a+5中得到x= , 为什么?反过来,能否从x=中得到(2a﹣1)x=3a+5,为什么?21. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个长为 ,宽为 的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示. (1)、能否用只含 的式子表示出图②中两块阴影部分的周长和?(填“能”或“不能”);(2)、若能,请你用只含 的式子表示出中两块阴影部分的周长和;若不能,请说明理由.22. 定义:若一个关于x的方程 的解为 ,则称此方程为“中点方程”.如: 的解为 ,而 ; 的解为 ,而 .(1)、若 ,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;(2)、若关于x的方程 是“中点方程”,求代数式 的值.23. 如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-12,点B表示10,点C表示20,我们称点A和点C在数轴上相距32个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒。则
(1)、能否用只含 的式子表示出图②中两块阴影部分的周长和?(填“能”或“不能”);(2)、若能,请你用只含 的式子表示出中两块阴影部分的周长和;若不能,请说明理由.22. 定义:若一个关于x的方程 的解为 ,则称此方程为“中点方程”.如: 的解为 ,而 ; 的解为 ,而 .(1)、若 ,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;(2)、若关于x的方程 是“中点方程”,求代数式 的值.23. 如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-12,点B表示10,点C表示20,我们称点A和点C在数轴上相距32个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着折线数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒。则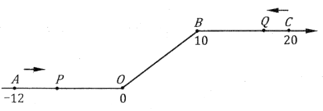 (1)、动点P从点A运动至点C需要时间多少秒?(2)、若P,Q两点在点M处相遇,则点M在折线数轴上所表示的数是多少?(3)、求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等。24. 小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.
(1)、动点P从点A运动至点C需要时间多少秒?(2)、若P,Q两点在点M处相遇,则点M在折线数轴上所表示的数是多少?(3)、求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等。24. 小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.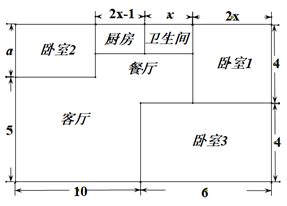 (1)、求a的值.(2)、铺设地面需要木地板和地砖各多少平方米(用含x的代数式表示)?(3)、按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有A、B两种活动方案,如表:
(1)、求a的值.(2)、铺设地面需要木地板和地砖各多少平方米(用含x的代数式表示)?(3)、按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有A、B两种活动方案,如表:活动方案
木地板价格
地砖价格
总安装费
A
8折
8.5折
2000元
B
9折
8.5折
免收
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?