初中数学浙教版七年级上册第五章 一元一次方程 单元检测(基础篇)
试卷更新日期:2020-09-26 类型:单元试卷
一、单选题
-
1. 下列方程中:① ,② ,③ ,④ ,⑤ ,⑥ 其中是一元一次方程的有( )A、5个 B、4个 C、3个 D、2个2. 若x=1是关于x的方程2x+a=1的解,则a的值为( )A、 B、1 C、3 D、3. 如图,相同形状的物体的重量是相等的,其中最左边天平是平衡的,则右边三个天平中仍然平衡的是( )
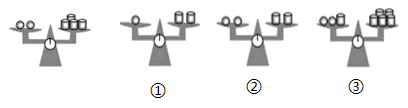 A、①②③ B、①③ C、①② D、②③4. 方程2x+1=﹣3和方程2﹣ =0的解相同,则a的值是( )A、8 B、4 C、3 D、55. 下列等式变形错误的是( )A、若x=y , 则x-5=y-5 B、若-3x=-3y , 则x=y C、若 = , 则x=y D、若mx=my , 则x=y6. 解方程 ,去括号正确的是( )A、 B、 C、
A、①②③ B、①③ C、①② D、②③4. 方程2x+1=﹣3和方程2﹣ =0的解相同,则a的值是( )A、8 B、4 C、3 D、55. 下列等式变形错误的是( )A、若x=y , 则x-5=y-5 B、若-3x=-3y , 则x=y C、若 = , 则x=y D、若mx=my , 则x=y6. 解方程 ,去括号正确的是( )A、 B、 C、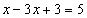 D、
7. 在解方程 时,去分母的过程正确的是( )A、 B、 C、 D、8. 一船由甲地开往乙地,顺水航行要4小时,逆水航行比顺水航行多用40分钟,已知船在静水中的速度为16千米/时,求水流速度. 解题时,若设水流速度为x千米/时,那么下列方程中正确的是( )A、 B、 C、 D、9. 已知某网络书店销售两套版本不同的《趣味数学丛书》,售价都是70元,其中一套盈利 ,另一套亏本 ,则在这次买卖中,网络书店的盈亏情况是( )A、盈利15元 B、盈利10元 C、不盈不亏 D、亏损10元10. 下列各个变形正确的是( )A、由 去分母,得 B、方程 可化为 C、由 去括号,得 D、由 去括号,移项,合并同类项,得
D、
7. 在解方程 时,去分母的过程正确的是( )A、 B、 C、 D、8. 一船由甲地开往乙地,顺水航行要4小时,逆水航行比顺水航行多用40分钟,已知船在静水中的速度为16千米/时,求水流速度. 解题时,若设水流速度为x千米/时,那么下列方程中正确的是( )A、 B、 C、 D、9. 已知某网络书店销售两套版本不同的《趣味数学丛书》,售价都是70元,其中一套盈利 ,另一套亏本 ,则在这次买卖中,网络书店的盈亏情况是( )A、盈利15元 B、盈利10元 C、不盈不亏 D、亏损10元10. 下列各个变形正确的是( )A、由 去分母,得 B、方程 可化为 C、由 去括号,得 D、由 去括号,移项,合并同类项,得二、填空题
-
11. 请写出一个解为 的一元一次方程:12. 若2m+n=25,m-2n=2,则(m+3n)2-(3m-n)2= .
13. 一个正数的两个平方根分别是2a-2和a-7,则这个正数是。14. 小新问妈妈的生日是几号?妈妈指着某月日历回答:我生日这一天的上、下、左、右四个日期数之和恰好是80,则小新妈妈的生日是号.15. 一部拖拉机耕一片地,第一天耕了这片地的 ;第二天耕了剩下部分的 ,还剩下 42公顷没耕完,则这片地共有公顷16. 规定:用 表示大于 的最小整数,例如 , , 等;用 表示不大于 的最大整数,例如 , , ,如果整数 满足关系式: ,则 .三、解答题
-
17.(1)、2(x﹣2)﹣3(4x﹣1)=9(1﹣x);(2)、 .18. 根据等式性质.回答下列问题;(1)、从ab=bc能否得到a=c.为什么?
(2)、从=能否得到a=c,为什么?
(3)、从ab=1能否得到a+1=+1,为什么?19. 在作解方程练习时,学习卷中有一个方程“ ”中的 没印清晰,小聪问老师,老师只是说:“ 是个有理数,该方程的解与方程 的解相同.”小聪很快补上了这个常数,聪明的你能补上这个常数吗?20. 列方程解应用题.明代商人程大位在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
 21.(1)、已知2x+x2y=2,求-3x2y-6x+7的值(2)、已知y=1是方程2 - (m-y)=2y的解,求关于x的方程m(x+4)=2mx-4的解.22. 已知方程6x-9=10x-45与方程3a-1=3(x+a)-2a的解相同.(1)、求这个相同的解;(2)、求a的值;(3)、若[m]表示不大于m的最大整数,求[- a-2]的值.23. 2020年高峡水库蓄水达到了177米的设计目标水位.据测算,蓄水达到177米目标水位后,高峡水库电站的年发电量将达到842.4亿千瓦时,比2017年要多发电20%.据资料显示,火力发电时每燃烧12吨标准原煤可发电2.5万千瓦时.(千瓦时为一种能量单位)(1)、求2017年高峡电站的年发电量;(2)、请计算高峡电站2020年全年发电量与2017年全年发电量相比,可为国家多节约标准原煤多少万吨?(3)、已知2019年全年发电量比2018年增加了10%,2018年与2019年的发电量之和比2017年发电量的2倍还多129亿千瓦时,求2018年和2019年高峡电站年发电量.24. 如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形 的边长是1米;
21.(1)、已知2x+x2y=2,求-3x2y-6x+7的值(2)、已知y=1是方程2 - (m-y)=2y的解,求关于x的方程m(x+4)=2mx-4的解.22. 已知方程6x-9=10x-45与方程3a-1=3(x+a)-2a的解相同.(1)、求这个相同的解;(2)、求a的值;(3)、若[m]表示不大于m的最大整数,求[- a-2]的值.23. 2020年高峡水库蓄水达到了177米的设计目标水位.据测算,蓄水达到177米目标水位后,高峡水库电站的年发电量将达到842.4亿千瓦时,比2017年要多发电20%.据资料显示,火力发电时每燃烧12吨标准原煤可发电2.5万千瓦时.(千瓦时为一种能量单位)(1)、求2017年高峡电站的年发电量;(2)、请计算高峡电站2020年全年发电量与2017年全年发电量相比,可为国家多节约标准原煤多少万吨?(3)、已知2019年全年发电量比2018年增加了10%,2018年与2019年的发电量之和比2017年发电量的2倍还多129亿千瓦时,求2018年和2019年高峡电站年发电量.24. 如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形 的边长是1米;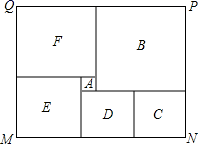 (1)、若设图中最大正方形 的边长是 米,请用含 的代数式分别表示出正方形 的边长(2)、观察图形的特点可知,长方形相对的两边是相等的(即 , )请根据以上结论,求出 的值(3)、现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
(1)、若设图中最大正方形 的边长是 米,请用含 的代数式分别表示出正方形 的边长(2)、观察图形的特点可知,长方形相对的两边是相等的(即 , )请根据以上结论,求出 的值(3)、现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?