初中数学浙教版九年级上册第四章 相似三角形 单元检测(提高篇)
试卷更新日期:2020-09-26 类型:单元试卷
一、单选题
-
1. 下列说法错误的是( )A、所有矩形都是相似的 B、若线段a=5cm,b=2cm,则a:b=5:2 C、若线段AB= cm,C是线段AB的黄金分割点,且AC>BC,则AC= cm D、四条长度依次为lcm,2cm,2cm,4cm的线段是成比例线段2. 一个三角形木架三边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm和120cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )A、一种 B、两种 C、三种 D、四种3. 如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( )
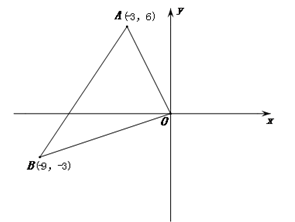 A、(-1,2) B、(-9,18) C、(-9,18)或(9,-18) D、(-1,2)或(1,-2)4.
A、(-1,2) B、(-9,18) C、(-9,18)或(9,-18) D、(-1,2)或(1,-2)4.如图,已知在 中, , , ,点 是 的重心,则点 到 所在直线的距离等于( )
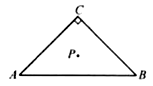 A、 B、 C、 D、5. 已知 ,则直线 一定经过的象限是( )A、第一、三、四象限 B、第一、二、四象限 C、第一、四象限 D、第二、三象限6. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )
A、 B、 C、 D、5. 已知 ,则直线 一定经过的象限是( )A、第一、三、四象限 B、第一、二、四象限 C、第一、四象限 D、第二、三象限6. 如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( ) A、 B、13 C、 D、7.
A、 B、13 C、 D、7.有3个正方形如图所示放置,阴影部分的面积依次记为S1 , S2 , 则S1:S2等于( )
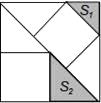 A、1: B、1:2 C、2:3 D、4:98. 下列命题正确的有( )个
A、1: B、1:2 C、2:3 D、4:98. 下列命题正确的有( )个①40°角为内角的两个等腰三角形必相似;
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为75°;
③一组对边平行,另一组对边相等的四边形是平行四边形;
④一个等腰直角三角形的三边是a、b、c , (a>b=c),那么a2:b2:c2=2:1:1;
⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c , 则此△为等腰直角三角形.
A、1个 B、2个 C、3个 D、4个9. 如图,P为反比例函数y= (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A,B.若∠AOB=135°,则k的值是( ) A、2 B、4 C、6 D、810. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
A、2 B、4 C、6 D、810. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )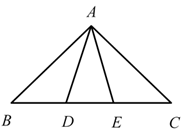 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 ,请再写出一条线段的长,使它与a、b这三条线段中的一条是另外两条的比例中项,则这条线段长为 .
12. 如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为时,△ADP和△ABC相似.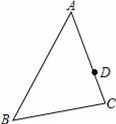 13. 如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .
13. 如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是 .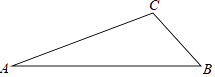 14. 在ΔABC 中,AC=4,BC=2. 点 D 在射线 AB 上,在构成的图形中,ΔACD 为等腰三角形,且存在两个互为相似的三角形,则 CD 的长是.15. 如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是.
14. 在ΔABC 中,AC=4,BC=2. 点 D 在射线 AB 上,在构成的图形中,ΔACD 为等腰三角形,且存在两个互为相似的三角形,则 CD 的长是.15. 如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是. 16. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.
16. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.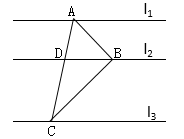
三、解答题
-
17.
如图,在△ABC中,AB=6cm , AC=12cm , 动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t , 使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
 18. 如图,在△ABC中,BC边上依次有B、D、E、C,AC边上依次有A、G、F,满足BD=CE= BC,CF=AG= AC,BF交AE于点J,交AD于I,BG交AE于点K,交AD于点H,且S△ABC=1,求S四边形KHIJ .
18. 如图,在△ABC中,BC边上依次有B、D、E、C,AC边上依次有A、G、F,满足BD=CE= BC,CF=AG= AC,BF交AE于点J,交AD于I,BG交AE于点K,交AD于点H,且S△ABC=1,求S四边形KHIJ . 19. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1 .
19. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1 . (1)、在图中标示出旋转中心P,并写出它的坐标;(2)、以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 , 在图中画出△A2B2C2 , 并写出C2的坐标.20.
(1)、在图中标示出旋转中心P,并写出它的坐标;(2)、以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2 , 在图中画出△A2B2C2 , 并写出C2的坐标.20.如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
 (1)、求线段CD的长;(2)、如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(1)、求线段CD的长;(2)、如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(3)、如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
21. 如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.设BE、CD的中点分别为P、Q. (1)、求AO的长;(2)、求PQ的长;(3)、设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.22. 在平面直角坐标系中,抛物线 与 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)、求AO的长;(2)、求PQ的长;(3)、设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.22. 在平面直角坐标系中,抛物线 与 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.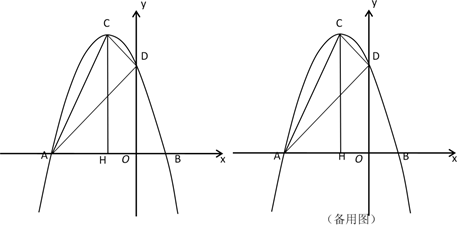 (1)、求抛物线的解析式和顶点C的坐标;(2)、连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;(3)、若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.23. 在 中, , .点D在边 上, 且 , 交边 于点F,连接 .
(1)、求抛物线的解析式和顶点C的坐标;(2)、连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;(3)、若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.23. 在 中, , .点D在边 上, 且 , 交边 于点F,连接 .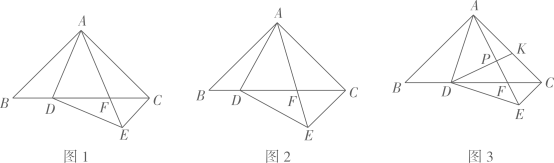 (1)、特例发现:如图1,当 时,①求证: ;②推断: ▲ .;(2)、探究证明:如图2,当 时,请探究 的度数是否为定值,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,当 时,过点D作 的垂线,交 于点P,交 于点K,若 ,求 的长.24. 如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F, 已知OB=8.
(1)、特例发现:如图1,当 时,①求证: ;②推断: ▲ .;(2)、探究证明:如图2,当 时,请探究 的度数是否为定值,并说明理由;(3)、拓展运用:如图3,在(2)的条件下,当 时,过点D作 的垂线,交 于点P,交 于点K,若 ,求 的长.24. 如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F, 已知OB=8.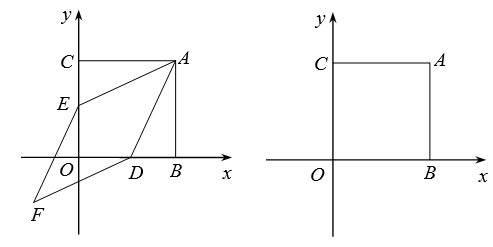 (1)、求证:四边形AEFD为菱形.(2)、求四边形AEFD的面积.(3)、若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.
(1)、求证:四边形AEFD为菱形.(2)、求四边形AEFD的面积.(3)、若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.