初中数学浙教版九年级上册第四章 相似三角形 章末检测(基础篇)
试卷更新日期:2020-09-26 类型:单元试卷
一、单选题
-
1. 已知点C是线段 的黄金分割点(其中 ), .则线段 的大小是( )A、 B、 C、 D、2. 若3x=2y(xy≠0),则下列比例式成立的是( )A、 B、 C、 D、3. 如图,已知一组平行线a//b//c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=2,BC=3,DE=1.6,则EF=( )
 A、2.4 B、1.8 C、2.6 D、2.84. 如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是( )
A、2.4 B、1.8 C、2.6 D、2.84. 如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是( )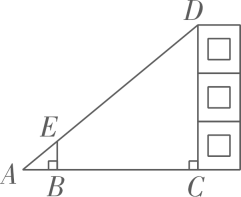 A、 B、 C、 D、5. 下列每组的两个图形中,不是位似图形的是( )A、
A、 B、 C、 D、5. 下列每组的两个图形中,不是位似图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列四条线段能成比例线段的是( )A、 B、 C、 D、7. 如果△ABC∽△DEF , A、B分别对应D、E , 且AB∶DE=1∶2,那么下列等式一定成立的是( )A、BC∶DE=1∶2 B、△ABC的面积∶△DEF的面积=1∶2 C、∠A的度数∶∠D的度数=1∶2 D、△ABC的周长∶△DEF的周长=1∶28. 如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
6. 下列四条线段能成比例线段的是( )A、 B、 C、 D、7. 如果△ABC∽△DEF , A、B分别对应D、E , 且AB∶DE=1∶2,那么下列等式一定成立的是( )A、BC∶DE=1∶2 B、△ABC的面积∶△DEF的面积=1∶2 C、∠A的度数∶∠D的度数=1∶2 D、△ABC的周长∶△DEF的周长=1∶28. 如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )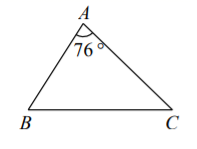 A、
A、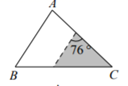 B、
B、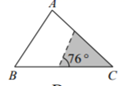 C、
C、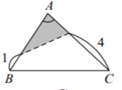 D、
D、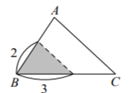 9. 点G是△ABC的重心,过点G画MN∥BC分别交AB;,AC于点MN,则△AMN与△ABC面积之比是( )A、 B、 C、
9. 点G是△ABC的重心,过点G画MN∥BC分别交AB;,AC于点MN,则△AMN与△ABC面积之比是( )A、 B、 C、 D、
D、 10. 如果一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是( )A、1: B、 :1 C、2:1 D、4:1
10. 如果一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是( )A、1: B、 :1 C、2:1 D、4:1二、填空题
-
11. 已知线段a=4,b=9,线段c是a,b的比例中项,则线段c=。12. 如图,△ABC与△DEF位似,位似中心为点O,且BC:EF=3:2,则S△ABC:S△DEF=.
 13. 如图,P为线段AB上一点,AD与BC交于E, ,BC交PD于F,AD交PC于G,则图中相似三角形有对.
13. 如图,P为线段AB上一点,AD与BC交于E, ,BC交PD于F,AD交PC于G,则图中相似三角形有对. 14. 如图,在△ABC中,D为AB边上的一点,要使△ABC~△AED成立,还需要添加一个条件为 .
14. 如图,在△ABC中,D为AB边上的一点,要使△ABC~△AED成立,还需要添加一个条件为 . 15. 在一张比例尺为1:50000的地图上,如果一块多边形地的周长是320cm,那么这块地的实际周长是km.16. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1 , △DEF的周长为C2 , 则 的值等于.
15. 在一张比例尺为1:50000的地图上,如果一块多边形地的周长是320cm,那么这块地的实际周长是km.16. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1 , △DEF的周长为C2 , 则 的值等于.
三、解答题
-
17. 已知线段a、b、c,且 .(1)、求 的值;(2)、若线段a、b、c满足 ,求a、b、c的值.18. 如图,菱形ABCD的边长为1,直线l过点C,交AB的延长线于M,交AD的延长线于N,求 的值.
 19. 如图,在等腰△ABC巾,AD是顶角∠BAC的角平分线,BE是腰AC边上的高,垂足为点E,求证:△ACD∽△BCE.
19. 如图,在等腰△ABC巾,AD是顶角∠BAC的角平分线,BE是腰AC边上的高,垂足为点E,求证:△ACD∽△BCE.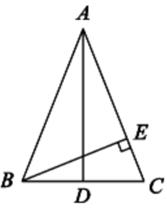 20. 如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.
20. 如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.求证:四边形AFGE与四边形ABCD相似.
 21. 在方格纸中,我们把像△ABC这样的顶点在小正方形的顶点的三角形叫做格点三角形.如图,左边的5×5的方格中有一个△ABC.
21. 在方格纸中,我们把像△ABC这样的顶点在小正方形的顶点的三角形叫做格点三角形.如图,左边的5×5的方格中有一个△ABC.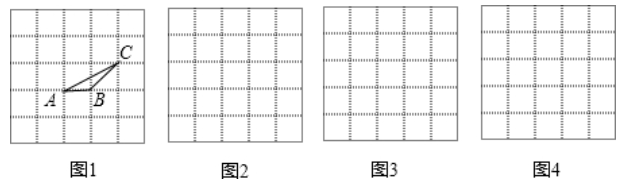 (1)、在右边三个5×5的方格纸中各画出一个与△ABC相似且互不全等的格点三角形
(1)、在右边三个5×5的方格纸中各画出一个与△ABC相似且互不全等的格点三角形
(2)、直接写出在一个6×6的方格纸中,可以画出的与△ABC相似的且互不全等的所有格点三角形的个数(不包括与△ABC全等的三角形)22. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (1)、①请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(1)、①请画出△ABC向左平移6个单位长度后得到的△A1B1C1;②以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2;
(2)、填空:△AA1A2的面积为.23. 如图,矩形 中, , ,点 在 上,连接 点 在直线 上, 交 于点 .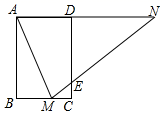 (1)、求证: 是等腰三角形;(2)、求证: ;(3)、当 为 中点时,求 的长.24. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度.
(1)、求证: 是等腰三角形;(2)、求证: ;(3)、当 为 中点时,求 的长.24. 淇淇和嘉嘉在习了利用相似三角形测高之后分别测量两个旗杆高度.(1)、如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E , 测得脚掌中心位置B到镜面中心C的距离是50cm , 镜面中心C距离旗杆底部D的距离为4m , 已知淇淇同的身高是1.54m , 眼睛位置A距离淇淇头顶的距离是4cm , 求旗杆DE 的高度. (2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度?
(2)、如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为 米,∠DCE=45°,求旗杆AB的高度?