初中数学浙教版九年级上册4.6相似多边形 同步练习
试卷更新日期:2020-09-26 类型:同步测试
一、单选题
-
1. 如果两个相似多边形的面积之比为1:4,那么它们的周长之比是( )
A、1:2 B、1:4 C、1:8 D、1:162. 西安市大雁塔广场占地面积约为667000m ,若按比例尺1∶2000缩小后,其面积大约相当于( )A、一个篮球场的面积 B、一张乒乓球台台面的面积 C、《华商报》的一个版面的面积 D、《数学》课本封面的面积3. 如图所示,在长为8 cm,宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( ) A、2 cm2 B、4 cm2 C、8 cm2 D、16 cm24. 如图,一张矩形报纸ABCD的长AB=a,宽BC=b,E,F分别是AB,CD的中点,将这张报纸沿着直线EF对折后,矩形AEFD的长与宽的比等于矩形ABCD的长与宽的比,则a:b等于( )
A、2 cm2 B、4 cm2 C、8 cm2 D、16 cm24. 如图,一张矩形报纸ABCD的长AB=a,宽BC=b,E,F分别是AB,CD的中点,将这张报纸沿着直线EF对折后,矩形AEFD的长与宽的比等于矩形ABCD的长与宽的比,则a:b等于( )
 A、 B、 C、 D、5. 下列各组图形一定相似的是( )A、两个直角三角形 B、两个等边三角形 C、两个菱形 D、两个矩形6. 如图所示的四边形,与选项中的四边形一定相似的是( )
A、 B、 C、 D、5. 下列各组图形一定相似的是( )A、两个直角三角形 B、两个等边三角形 C、两个菱形 D、两个矩形6. 如图所示的四边形,与选项中的四边形一定相似的是( ) A、
A、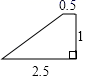 B、
B、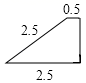 C、
C、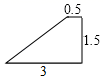 D、
D、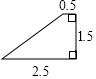 7. 下列说法中正确的是( )
7. 下列说法中正确的是( )①在两个边数相同的多边形中,如果对应边成比例,那么这两个多边形相似;②如果两个矩形有一组邻边对应成比例,那么这两个矩形相似;③有一个角对应相等的平行四边形都相似;④有一个角对应相等的菱形都相似.
A、①② B、②③ C、③④ D、②④8. 两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积和为78cm2 , 那么较大多边形的面积为( )A、46.8 cm2 B、42 cm2 C、52 cm2 D、54 cm29. 如图,矩形ABCD∽矩形FAHG,连结BD,延长GH分别交BD、BC于点Ⅰ、J,延长CD、FG交于点E,一定能求出△BIJ面积的条件是( )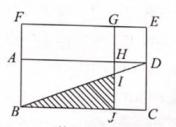 A、矩形ABJH和矩形HJCD的面积之差 B、矩形ABJH和矩形HDEG的面积之差 C、矩形ABCD和矩形AHGF的面积之差 D、矩形FBJG和矩形GJCE的面积之差10. 书画经装裱后更便于收藏.如图,画心ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A′B′C′D′,两矩形的对应边互相平行,且AB与A′B'的距离、CD与C′D′的距离都等于4cm . 当AD与A′D′的距离、BC与B'C′距离都等于acm , 且矩形ABCD∽矩形A′B′C′D'时,整幅书画最美观此时,a的值为( )
A、矩形ABJH和矩形HJCD的面积之差 B、矩形ABJH和矩形HDEG的面积之差 C、矩形ABCD和矩形AHGF的面积之差 D、矩形FBJG和矩形GJCE的面积之差10. 书画经装裱后更便于收藏.如图,画心ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A′B′C′D′,两矩形的对应边互相平行,且AB与A′B'的距离、CD与C′D′的距离都等于4cm . 当AD与A′D′的距离、BC与B'C′距离都等于acm , 且矩形ABCD∽矩形A′B′C′D'时,整幅书画最美观此时,a的值为( ) A、4 B、6 C、12 D、24
A、4 B、6 C、12 D、24二、填空题
-
11. 一个四边形的边长分别是3,4,5,6,另一个与它相似的四边形最小边长为6,则另一个四边形的最长边是.12. 把一个长方形按如图方式划分成三个全等的小长方形,每一个小长方形与原长方形相似,若小长方形的宽为2,则原长方形的宽x为。
 13. 以小正方形的中心为位似中心,以1:3的比例放大得到一个大正方形,从而得到了一个如图所示的飞镖游戏板.若小明同学向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则镖落在阴影部分的概率是.
13. 以小正方形的中心为位似中心,以1:3的比例放大得到一个大正方形,从而得到了一个如图所示的飞镖游戏板.若小明同学向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则镖落在阴影部分的概率是. 14. 如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为 ,连接CF,则CF=.
14. 如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为 ,连接CF,则CF=.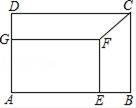
三、解答题
-
15. 如图,左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形,要求大小与左边四边形不同.
 16. 如图,四边形ABCD∽四边形A′B′C′D′.
16. 如图,四边形ABCD∽四边形A′B′C′D′. (1)、α=(2)、求边x、y的长度.17. 一个矩形ABCD的较短边长为2.
(1)、α=(2)、求边x、y的长度.17. 一个矩形ABCD的较短边长为2.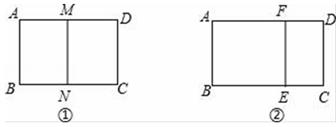 (1)、如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;(2)、如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.18. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)、如图①,若沿长边对折后得到的矩形与原矩形相似,求它的另一边长;(2)、如图②,已知矩形ABCD的另一边长为4,剪去一个矩形ABEF后,余下的矩形EFDC与原矩形相似,求余下矩形EFDC的面积.18. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.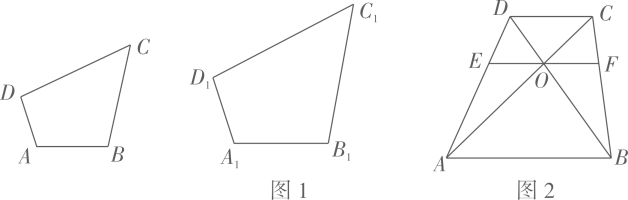 (1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
(1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).①条边成比例的两个凸四边形相似;(命题)
②三个角分别相等的两个凸四边形相似;(命题)
③两个大小不同的正方形相似.(命题)
(2)、如图1,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1 , ∠BCD=∠B1C1D1 , ,求证:四边形ABCD与四边形A1B1C1D1相似.(3)、如图2,四边形ABCD中,AB∥CD , AC与BD相交于点O , 过点O作EF∥AB分别交AD , BC于点E , F . 记四边形ABFE的面积为S1 , 四边形EFDE的面积为S2 , 若四边形ABFE与四边形EFCD相似,求 的值.