初中数学浙教版九年级上册4.5相似三角形的性质及应用（3）同步练习
试卷更新日期：2020-09-26 类型：同步测试
一、单选题
-
1. 如图，小明同学用自制的直角三角形纸板 测量树的高度 ，他调整自己的位置，设法使斜边 保持水平，并且边 与点 在同一直线上.已知纸板的两条直角边 ， ，测得边 离地面的高度 ， ，则树高 是（ ）
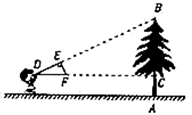A、4米 B、4.5米 C、5米 D、5.5米2. 身高1.6米的小明同学利用相似三角形测量学校旗杆的高度，上午10点，小明在阳光下的影长为1米，此时测得旗杆的影长为9米，则学校旗杆的高度是（ ）A、 米 B、 米 C、 米 D、 米3. 路边有一根电线杆AB和一块长方形广告牌，有一天小明突然发现在太阳光照射下，电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处，而长方形广告牌的影子刚好落在地面上E点（如图），已知BC=5米，长方形广告牌的长HF=4米，高HC=3米，DE=4米，则电线杆AB的高度是（ ）
A、6.75米 B、7.75米 C、8.25米 D、10.75米4. AB和DE是直立在水平地面上的两根立柱，AB=7米，某一时刻测得在阳光下的投影 米，同时，测量出 在阳光下的投影长为6米，则DE的长为（ ）A、 米 B、 米 C、 米 D、 米5. 如图，为了估计某一条河的宽度，在河的对岸选定一个目标点P，在近岸取点Q和S，使点P，Q，S在一条直线上，且直线PS与河垂直，在过点S且与PS垂直的直线a上选择适当的点T，PT与过点Q且与PS垂直的直线b的交点为R，如果QS = 60m，ST =120m，QR=80m，则这条河的宽度PQ为（ ）
A、40m B、120m C、60m D、180m6. 现有一个测试距离为5m的视力表(如图)，根据这个视力表，小华想制作一个测试距离为3m的视力表，则图中的 的值为（ ）
A、 B、 C、 D、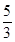
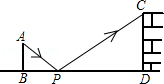
7. 如图，小明为了测量高楼MN的高度，在离N点20米的A处放了一个平面镜，小明沿NA方向后退1.5米到C点，此时从镜子中恰好看到楼顶的M点，已知小明的眼睛（点B）到地面的高度BC是1.6米，则大楼MN的高度（精确到0.1米）约是（ ）
A、18.75米 B、18.8米 C、21.3米 D、19米8. 据《九章算术》记载：“今有山居木西，不知其高.山去五十三里，木高九丈五尺.人立木东三里，望木末适与山峰斜平.人目高七尺.问山高几何？”译文如下：如图，今有山 位于树的西面.山高 为未知数，山与树相距53里，树高9丈5尺.人站在离树3里的地方，观察到树梢C恰好与山峰A处在同一条直线上，人眼离地7尺.则山高 的长为（结果保留到整数，1丈=10尺）（ ）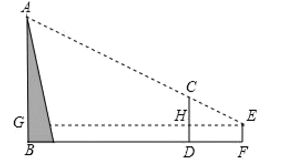
A、162丈 B、163丈 C、164丈 D、165丈9. 如图，有一块三角形土地，它的底边 米，高 米，某单位要沿着底边 修一座底面是矩形 的大楼，矩形的长宽比为5：4，则这座大楼的地基面积是（ ）
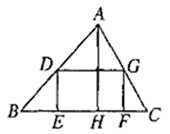A、 B、 C、 D、10. 如图所示，某超市在一楼至二楼之间安装有电梯，天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过，请你根据图中数据回答，两层楼之间的高约为（ ）
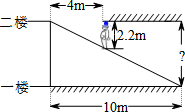A、 B、 C、11m D、二、填空题
-
11. 如图是小玲用手电来测量城墙高度的示意图．在点P处水平放置平面镜，光线从点A出发经平面镜反射后，刚好射到城墙CD的顶端C处．已知AB⊥BD，CD⊥BD，且测得AB＝1.4米，BP＝2.1米，PD＝12米，则该城墙CD的高度米．
12. 我军侦察员在距敌方AN=120m的地方发现敌方的一座建筑物，但不知其高度，又不能靠近建筑物测量，机灵的侦察员将自己的食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住，如图所示.若此时眼睛到食指的距离AM约为40cm，食指BC的长约为8cm，则敌方建筑物DE的高度约是m。
13. 图1是小红在“淘宝·双11”活动中所购买的一张多档位可调节靠椅，档位调节示意图如图2所示。已知两支脚AB=AC，为AC上固定连接点，靠背OD=10分米。档位为Ⅰ档时，OD∥AB，档位为Ⅱ挡时，OD’⊥AC。当靠椅由Ⅰ档调节为Ⅱ档时，靠背顶端D向后靠至D’，此时点D移动的水平距离是2分米，即ED’=2分米。DE⊥BC交OD’于点G，则DG=分米。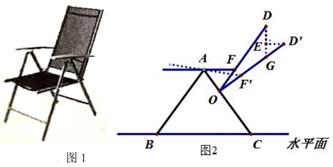
14. 如图，火焰的光线穿过小孔O，在竖直的屏幕上形成倒立的实像，像的长度BD=2 cm，OA=60 cm， OB=15 cm，则火焰的长度为.
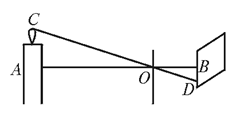15. 如图所示为农村一古老的捣碎器，已知支撑柱 的高为 米，踏板 长为 米，支撑点 到踏脚 的距离为 米，现在踏脚着地，则捣头点 上升了米．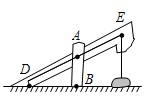
三、解答题
-
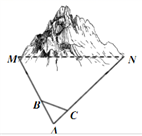
16. 中国高铁近年来用震惊世界的速度不断发展，已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图，某高铁在修建时需打通一直线隧道MN(M、N为山的两侧)，工程人员为了计算MN两点之间的直线距离，选择了在测量点A、B、C进行测量，点B、C分别在AM、AN上，现测得AM=1200米，AN=2000米，AB=30米，BC=45米，AC=18米，求直线隧道MN的长。
17. 如图，是小亮晚上在广场散步的示意图，图中线段AB表示站立在广场上的小亮，身高为1.6m，线段PO表示直立在广场上的灯杆，点P表示照明灯的位置．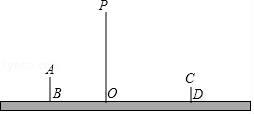
(1)、在小亮由B处沿BO所在的方向行走到达O处的过程中，他在地面上的影子长度越来越（用“长”或“短”填空）；请你在图中分别画出小亮站在B处、D处的影子；(2)、当小亮离开灯杆的距离OB＝3.6m时，小亮的影长为1.2m，灯杆的高度为多少m？(3)、当小亮离开灯杆的距离OD＝6m时，小亮的影长变为多少m？18. 如图，小芳家的落地窗（线段DE）与公路（直线PQ）互相平行，她每天做完作业后都会在点A处向窗外的公路望去．
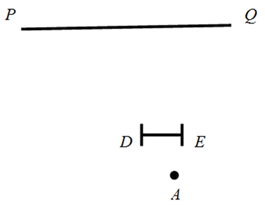(1)、请在图中画出小芳能看到的那段公路并记为BC．(2)、小芳很想知道点A与公路之间的距离，于是她想到了一个办法．她测出了邻家小彬在公路BC段上走过的时间为10秒，又测量了点A到窗的距离是4米，且窗DE的长为3米，若小彬步行的平均速度为1.2米/秒，请你帮助小芳计算出点A到公路的距离．19. 有一块锐角三角形卡纸余料ABC，它的边BC＝120 cm，高AD＝80 cm，为使卡纸余料得到充分利用，现把它裁剪成一个邻边之比为2∶5的矩形纸片EFGH和正方形纸片PMNQ，裁剪时，矩形纸片的较长边在BC上，正方形纸片一边在矩形纸片的较长边EH上，其余顶点均分别在AB，AC上，具体裁剪方式如图所示．
(1)、求矩形纸片较长边EH的长.(2)、裁剪正方形纸片时，小聪同学是按以下方法进行裁剪的：先沿着剩余料△AEH中与边EH平行的中位线剪一刀，再沿过该中位线两端点向边EH所作的垂线剪两刀，请你通过计算，判断小聪的剪法是否正确．