初中数学浙教版九年级上册4.5相似三角形的性质及应用(2)同步练习
试卷更新日期:2020-09-26 类型:同步测试
一、单选题
-
1. 两个相似三角形,其面积比为16:9,则其相似比为( )A、16:9 B、4:3 C、9:16 D、3:42. 若两个相似三角形的周长之比为1∶4,则它们的面积之比为( )A、1∶2 B、1∶4 C、1∶8 D、1∶163. 已知 ,它们的周长分别为30和15,且 ,则 的长为A、3 B、2 C、4 D、54. 已知△ABC∽△DEF,△ABC与△DEF面积之比为1
 4.若BC=1,则EF的长是( ) A、2 B、2 C、4 D、165. 已知△ABC∽△DEF , 若△ABC与△DEF的相似比为2:3,△ABC的面积为40,则△DEF的面积为( )A、60 B、70 C、80 D、906. 如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )
4.若BC=1,则EF的长是( ) A、2 B、2 C、4 D、165. 已知△ABC∽△DEF , 若△ABC与△DEF的相似比为2:3,△ABC的面积为40,则△DEF的面积为( )A、60 B、70 C、80 D、906. 如图,在△ABC中,点D,E分别是边AB,BC的中点,若△DBE的周长是7,则△ABC的周长是( )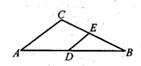 A、8 B、10 C、12. D、147. 如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2 , △OAB与△OCD的周长分别是C1和C2 , 则下列等式一定成立的是( )
A、8 B、10 C、12. D、147. 如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2 , △OAB与△OCD的周长分别是C1和C2 , 则下列等式一定成立的是( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90°, CD⊥AB,垂足为点D,如果 ,AD=9,那么BC的长是( )
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90°, CD⊥AB,垂足为点D,如果 ,AD=9,那么BC的长是( )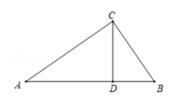 A、4 B、6 C、2 D、39. 如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.
A、4 B、6 C、2 D、39. 如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.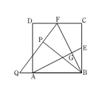
①AE⊥BF; ②QB=QF; ③ ; ④SECPG=3S△BGE
A、1 B、4 C、3 D、210. 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB,若AB=3BD。则S△ADE:S△EFC的值为( )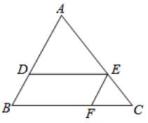 A、4:1 B、3:2 C、2:1 D、3:1
A、4:1 B、3:2 C、2:1 D、3:1二、填空题
-
11. 如图,已知△ABC∽△DBE,AB=6,DB=8,则 =.
 12. 公园中儿童游乐场是两个相似三角形地块,相似比为2:3,其中大三角形地块面积为27,则小三角形地块的面积是.13. 如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB=。
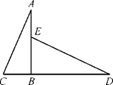
12. 公园中儿童游乐场是两个相似三角形地块,相似比为2:3,其中大三角形地块面积为27,则小三角形地块的面积是.13. 如图,在△ABC中,D、E分别是边AB、AC上的点,且DE∥BC,若△ADE与△ABC的周长之比为2:3,AD=4,则DB=。 14. 如图,在 中,点E是 的中点, , 的延长线交于点F.若 的面积为1,则四边形 的面积为.
14. 如图,在 中,点E是 的中点, , 的延长线交于点F.若 的面积为1,则四边形 的面积为.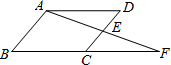 15. 如图,图①是一块边长为1,面积记为 的正三角形纸板,沿图①的底边剪去一块边长为 的正三角形纸板后得到图②,剪下的正三角纸板面积记为 ,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 后,得图③、④,…,记剪下的第2019块小正三角形纸板的面积为 ,则 等于.
15. 如图,图①是一块边长为1,面积记为 的正三角形纸板,沿图①的底边剪去一块边长为 的正三角形纸板后得到图②,剪下的正三角纸板面积记为 ,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 后,得图③、④,…,记剪下的第2019块小正三角形纸板的面积为 ,则 等于.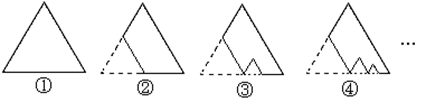
三、解答题
-
16. 已知 和 中,有 ,且 和 的周长之差为15厘米,求 和 的周长.17. △ABC∽△A`B`C`, ,边上的中线CD=4cm,△ABC的周长为20cm,△A`B`C`的面积是64 cm2 , 求:(1)、A`B`边上的中线C`D`的长;(2)、△A`B`C`的周长(3)、△ABC的面积18. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(﹣2,0),点B(4,0),与y轴交于点C(0,8),连接BC,又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从O运动到B(不含O点和B点),且分别交抛物线、线段BC以及x轴于点P,D,E.
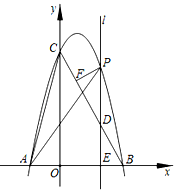 (1)、求抛物线的表达式;(2)、连接AC,AP,当直线l运动时,求使得△PEA和△AOC相似的点P的坐标;(3)、作PF⊥BC,垂足为F,当直线l运动时,求Rt△PFD面积的最大值.
(1)、求抛物线的表达式;(2)、连接AC,AP,当直线l运动时,求使得△PEA和△AOC相似的点P的坐标;(3)、作PF⊥BC,垂足为F,当直线l运动时,求Rt△PFD面积的最大值.