初中数学浙教版九年级上册4.4 相似三角形的判定（2）同步练习

试卷更新日期：2020-09-26 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，在Rt△ABC中，∠C=90°.CD是斜边AB上的高，若得到CD²=BD•AD这个结论可证明（　　）

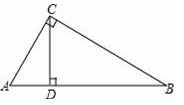A、△ADC∽△ACB B、△BDC∽△BCA C、△ADC∽△CDB D、无法判断

查看试题解析
2. 如图，下列条件中，不能判定△ACD∽△ABC的是（）

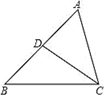A、∠ADC＝∠ACB B、∠B＝∠ACD C、∠ACD＝∠BCD D、 $\frac{A C}{A B} = \frac{A D}{A C}$

查看试题解析
3. 如图，点 $D$ 、 $E$ 分别在 $△ A B C$ 的边 $A B$ 、 $A C$ 上，且 $D E$ 与 $B C$ 不平行．下列条件中，能判定 $△ A D E$ 与 $△ A C B$ 相似的是（　　）

A、 $\frac{A D}{A C} = \frac{A E}{A B}$ B、 $\frac{A D}{A E} = \frac{A B}{A C}$ C、 $\frac{D E}{B C} = \frac{A E}{A B}$ D、 $\frac{D E}{B C} = \frac{A D}{A C}$

查看试题解析
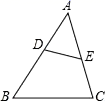4. 如图，△ABC中∠A=60°，AB=4，AC=6，将△ABC沿图示中的虚线剪开，剪下的三角形与△ABC不相似的是（）

A、 B、 C、 D、

查看试题解析
5. 已知：如图，Rt△ABC中，∠BAC=90°，D是AC上一点，∠ABD=∠C，直线EF过点D，与BA的延长线相交于F，且EF⊥BC，垂足为E.则图中所有与△ABD相似的三角形有多少个（）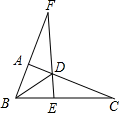

A、3 B、4 C、5 D、6

查看试题解析
6. 如图，在△ABC中，D是边AC上一点，联结BD，给出下列条件：∠ABD=∠ACB；②AB²=AD•AC；③AD•BC=AB•BD；④AB•BC=AC•BD．其中单独能够判定△ABD∽△ACB的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，已知△ABC和△PBD都是正方形网格上的格点三角形（顶点为网格线的交点），要使△ABC∽△PBD ，则点P的位置应落在（）

A、点P₁上 B、点P₂上 C、点P₃上 D、点P₄上

查看试题解析
8. 如图，四边形ABCD的对角线AC、BD相交于O，且将这个四边形分成①、②、③、④四个三角形．若OA：OC=OB：OD，则下列结论中一定正确的是（）

A、①与②相似 B、①与③相似 C、①与④相似 D、②与④相似

查看试题解析
9. 如图，在△ABC中，P为AB上一点，有下列四个条件：①∠B＝∠ACP；②∠APC＝∠ACB；③AC²＝AP·AB；④AB·CP＝AP·CB.其中能使△APC和△ACB相似的条件是（）

A、①②④ B、①③④ C、②③④ D、①②③

查看试题解析
10. 如图所示，在等边△ABC中，点D，E分别在AC，AB上，且 $\frac{A D}{A C}$ ＝ $\frac{1}{3}$ ，AE＝BE，则有（）

A、△AED∽△BED B、△AED∽△CBD C、△AED∽△ABD D、△BAD∽△BCD

查看试题解析
11. 如图，正方形ABCD的边长AB=8，E为平面内一动点，且AE=4，F为CD上一点，CF=2，连接EF，ED，则2EF+ED的最小值为（）

A、12 $\sqrt{3}$ B、12 $\sqrt{2}$ C、12 D、10

查看试题解析

二、填空题

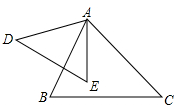
12. 如图，在△ABC和△ADE中， $\frac{A B}{B C}$ = $\frac{A E}{E D}$ ，要使△ABC 和 △ADE相似，还需要添加一个条件，这个条件是

查看试题解析
13. 如图，正方形ABCD中，E是CD的中点，P是BC上一点，要使ΔABP与ΔECP相似，还需具备的一个条件是.

查看试题解析
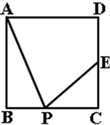14. 如图，AD∥BC，∠D=90°，AD=2，BC=6，DC=8，若在边DC上有点P，使△PAD与△PBC相似，则这样的点P有个．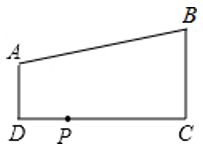

查看试题解析

三、解答题

15. 如图，在△ABC中，点D，E分别在边AB，AC上，∠AED＝∠B，线段AG分别交线段DE，BC于点F，G，且 $\frac{A D}{A C}$ ＝ $\frac{D F}{C G}$ ．

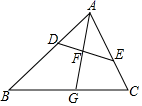(1)、求证：△ADF∽△ACG；

(2)、若 $\frac{A D}{A C}$ ＝ $\frac{3}{7}$ ，求 $\frac{AF}{FG}$ 的值．

查看试题解析
16. 如图，在矩形ABCD中，AB：BC=1：2，点E在AD上，且ED=3AE.判断△ABC与△EAB是否相似，并说明理由.

查看试题解析
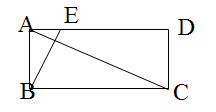17. 在△ABC中，AB=4cm，BC=8cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，如果P、Q分别从A、B同时出发，经几秒后，点P、B、Q构成的三角形△PBQ与△ABC相似?

查看试题解析
18. 如图，直线 $y = - x + 3$ 与 $x$ 轴、 $y$ 轴分别相交于点B、C，经过B、C两点的抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴的另一个交点为A，顶点为P，且对称轴为直线 $x = 2$ 。点G是抛物线 $y = a x^{2} + b x + c$ 位于直线 $y = - x + 3$ 下方的任意一点，连接PB、GB、GC、AC.

(1)、求该抛物线的解析式；

(2)、求△GBC面积的最大值；

(3)、连接AC，在 $x$ 轴上是否存在一点Q，使得以点P，B，Q为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由。

查看试题解析