初中数学浙教版九年级上册4.4 相似三角形的判定(1)同步练习
试卷更新日期:2020-09-26 类型:同步测试
一、单选题
-
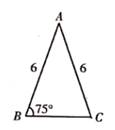
1. 下列各组条件中,不能判定△ABC与△A′B′C′相似的是( )A、∠A=∠A′,∠B=∠B′ B、∠C=∠C′=90°,∠A=12°,∠B′=78° C、∠A=∠B,∠B′=∠A′ D、∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′2. 已知△ABC如图所示,则下面四个三角形中与△ABC相似的是( )
 A、
A、 B、
B、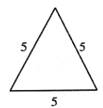 C、
C、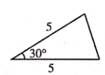 D、
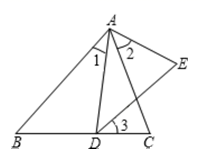
D、 3. 已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )A、一定不相似 B、不一定相似 C、一定相似 D、不能确定4. 如图,∠1=∠2,DE∥AC,则图中的相似三角形有( )
3. 已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是40°,80°,则这两个三角形( )A、一定不相似 B、不一定相似 C、一定相似 D、不能确定4. 如图,∠1=∠2,DE∥AC,则图中的相似三角形有( )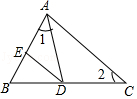 A、2对 B、3对 C、4对 D、5对5. 如图,△ABC中,D,E分别为AB,AC上的点,如果∠1=∠2=∠3,那么图中的相似三角形共有( )对.
A、2对 B、3对 C、4对 D、5对5. 如图,△ABC中,D,E分别为AB,AC上的点,如果∠1=∠2=∠3,那么图中的相似三角形共有( )对.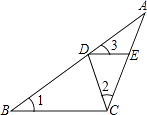 A、2 B、3 C、4 D、56. 如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,(1) ∠AED=∠B(2) (3) ,使△ADE与△ACB一定相似( )
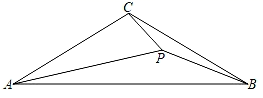
A、2 B、3 C、4 D、56. 如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,(1) ∠AED=∠B(2) (3) ,使△ADE与△ACB一定相似( )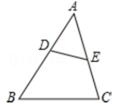 A、(1)(2) B、(2) C、(1)(3) D、(1)(2)(3)7. 如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC与点G,则下列结论中错误的是( )
A、(1)(2) B、(2) C、(1)(3) D、(1)(2)(3)7. 如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC与点G,则下列结论中错误的是( ) A、△CGE∽△CBP B、△APD∽△PGD C、△APG∽△BFP D、△PCF∽△BCP8. 如图,在 中,高 相交于点 ,图中与 相似的三角形共有( )
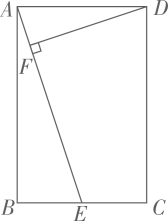
A、△CGE∽△CBP B、△APD∽△PGD C、△APG∽△BFP D、△PCF∽△BCP8. 如图,在 中,高 相交于点 ,图中与 相似的三角形共有( )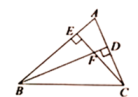 A、1个 B、2个 C、3个 D、4个9. 已知△ABC是正三角形,点D是边AC上一动点(不与A、C重合),以BD为边作正△BDE,边DE与边AB交于点F,则图中一定相似的三角形有( )对
A、1个 B、2个 C、3个 D、4个9. 已知△ABC是正三角形,点D是边AC上一动点(不与A、C重合),以BD为边作正△BDE,边DE与边AB交于点F,则图中一定相似的三角形有( )对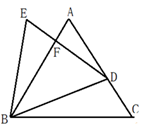 A、6 B、5 C、4 D、310. 如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是( )
A、6 B、5 C、4 D、310. 如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是( )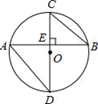 A、AE>BE B、 = C、∠D= ∠AEC D、△ADE∽△CBE
A、AE>BE B、 = C、∠D= ∠AEC D、△ADE∽△CBE二、填空题
-
11. 如图,点 在 的边 上,请你添加一个条件,使得 ∽ ,这个条件可以是.
 12. 如图,∠BAC=80°,∠B=40°,∠E=60°,若将图中的△ADE旋转(平移),则所得到的新三角形与△ABC , 与△ADE
12. 如图,∠BAC=80°,∠B=40°,∠E=60°,若将图中的△ADE旋转(平移),则所得到的新三角形与△ABC , 与△ADE 13. 如图,在▱ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F , 且CF=1,则CE的长为 .
13. 如图,在▱ABCD中,AB=3,AD=5,AF分别交BC于点E、交DC的延长线于点F , 且CF=1,则CE的长为 .
三、解答题
-
14. 如图,已知 ,则 相似吗?说明理由。
 15. 如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
15. 如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.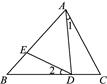 16. 如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,求证:△ABC∽△DEF.
16. 如图,已知在△ABC与△DEF中,∠C=54°,∠A=47°,∠F=54°,∠E=79°,求证:△ABC∽△DEF.