河北省邢台市桥东区2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 如果把向东走3km记作+3km , 那么﹣2km表示的实际意义是( )A、向东走2km B、向西走2km C、向南走2km D、向北走2km2. 下图几何体面的个数为( )
 A、1 B、2 C、3 D、43. 表示的意义是( )A、-4的相反数是4 B、表示4的点到原点的距离是4 C、4的相反数是-4 D、表示-4的点到原点的距离是44. 如图,下面四种表示角的方法,其中正确的是( )
A、1 B、2 C、3 D、43. 表示的意义是( )A、-4的相反数是4 B、表示4的点到原点的距离是4 C、4的相反数是-4 D、表示-4的点到原点的距离是44. 如图,下面四种表示角的方法,其中正确的是( ) A、∠A B、∠B C、∠C D、∠D5. 若 ,则 的值是( )A、 B、 C、2 D、-26. 在正常情况下,射击时要保证瞄准的一只眼在准星和缺口确定的直线上,才能射中目标,这样做的依据是( )
A、∠A B、∠B C、∠C D、∠D5. 若 ,则 的值是( )A、 B、 C、2 D、-26. 在正常情况下,射击时要保证瞄准的一只眼在准星和缺口确定的直线上,才能射中目标,这样做的依据是( ) A、两点之间线段最短 B、两点确定一条直线 C、三点确定一条直线 D、四点确定一条直线7. 2018年1月24日是腊八节,这天哈尔滨市的最低气温是﹣35℃,最高气温是﹣24℃,这一天哈尔滨市的温差为( )
A、两点之间线段最短 B、两点确定一条直线 C、三点确定一条直线 D、四点确定一条直线7. 2018年1月24日是腊八节,这天哈尔滨市的最低气温是﹣35℃,最高气温是﹣24℃,这一天哈尔滨市的温差为( )
A、 9℃ B、10℃ C、11℃ D、59℃8. 下面四幅图中,用量角器测得∠AOB度数是40°的图是( )A、 B、
B、 C、
C、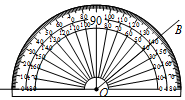 D、
D、 9. 如图是佳佳的作业,他用了简便方法,依据是( )
9. 如图是佳佳的作业,他用了简便方法,依据是( )解:原式=
=
=
= .
A、乘法交换律 B、乘法交换律与乘法分配律 C、乘法分配律 D、乘法结合律与乘法交换律10. 下列式子可读作:“负1,负3,正6,负8的和”的是( )A、 B、 C、 D、11. 如图,点 、 、 、 、 都在方格子的格点上,若 是由 绕点 按顺时针方向旋转得到的,则旋转的角度为( ) A、60° B、135° C、45° D、90°12. 在 中用数字 替换其中一个非 数码后,使所得的数最小,则被替换的数字是( )A、8 B、3 C、2 D、113. 用直尺和圆规作∠HDG=∠AOB的过程,弧①是( )
A、60° B、135° C、45° D、90°12. 在 中用数字 替换其中一个非 数码后,使所得的数最小,则被替换的数字是( )A、8 B、3 C、2 D、113. 用直尺和圆规作∠HDG=∠AOB的过程,弧①是( ) A、以D为圆心,以DN为半径画弧 B、以D为圆心,以EF为半径画弧 C、以M为圆心,以DN为半径画弧 D、以M为圆心,以EF为半径画弧14. 一根 长的绳子,第一次剪去绳子的 ,第二次剪去剩下绳子的 ,如此剪下去,第100次剪完后剩下绳子的长度是( )A、 B、 C、 D、
A、以D为圆心,以DN为半径画弧 B、以D为圆心,以EF为半径画弧 C、以M为圆心,以DN为半径画弧 D、以M为圆心,以EF为半径画弧14. 一根 长的绳子,第一次剪去绳子的 ,第二次剪去剩下绳子的 ,如此剪下去,第100次剪完后剩下绳子的长度是( )A、 B、 C、 D、二、填空题
-
15. 如图是校园花圃一角,有的同学为了省时间图方便,在花圃中踩出了一条小道,这些同学这样做的数学道理是 .
 16. 一副三角板按如下图方式摆放,若 ,则 的度数为 . 只用度表示 的补角为 .
16. 一副三角板按如下图方式摆放,若 ,则 的度数为 . 只用度表示 的补角为 . 17. 现有七个数﹣1,﹣2,﹣2,﹣4,﹣4,﹣8,﹣8将它们填入图1(3个圆两两相交分成7个部分)中,使得每个圆内部的4个数之积相等,设这个积为m,如图2给出了一种填法,此时m=64,在所有的填法中,m的最大值为.
17. 现有七个数﹣1,﹣2,﹣2,﹣4,﹣4,﹣8,﹣8将它们填入图1(3个圆两两相交分成7个部分)中,使得每个圆内部的4个数之积相等,设这个积为m,如图2给出了一种填法,此时m=64,在所有的填法中,m的最大值为.
三、解答题
-
18.(1)、如下图,下而两个圈分别表示负数集和分数集,请你把下列各数填入它所在的数集的圈里:
 (2)、上图中,这两个圈的重叠部分表示什么数的集合?19. 如图,平面上有四个点A,B,C,D,根据下列语句画图:
(2)、上图中,这两个圈的重叠部分表示什么数的集合?19. 如图,平面上有四个点A,B,C,D,根据下列语句画图: (1)、画线段AC、BD交于E点;(2)、作射线BC;(3)、取一点P,使点P既在直线AB上又在直线CD上.
(1)、画线段AC、BD交于E点;(2)、作射线BC;(3)、取一点P,使点P既在直线AB上又在直线CD上.
20. 在一条不完整的数轴上从左到右有点A , B , C , 其中AB=2cm , BC=4cm , 设点A , B , C所对应的数的和是p .(1)、若以B为原点,2cm长为一个单位长度,写出点A、C所对应的数,并计算p的值;(2)、若原点O为BC的中点,以1cm长为一个单位长度,求p .21. 计算:(1)、(2)、22. 如图,C为线段AD上一点,点B为CD的中点,且 , (1)、求AC的长(2)、若点E在直线AD上,且 ,求 的长23. 旭东中学附近某水果超市最近新进了一批百香果,每斤8元,为了合理定价,在第一周试行机动价格,卖出时每斤以10元为标准,超出10元的部分记为正,不足10元的部分记为负,超市记录第一周百香果的售价情况和售出情况:
(1)、求AC的长(2)、若点E在直线AD上,且 ,求 的长23. 旭东中学附近某水果超市最近新进了一批百香果,每斤8元,为了合理定价,在第一周试行机动价格,卖出时每斤以10元为标准,超出10元的部分记为正,不足10元的部分记为负,超市记录第一周百香果的售价情况和售出情况:星期
一
二
三
四
五
六
日
每斤价格相对于标准价格(元)
+1
﹣2
+3
﹣1
+2
+5
﹣4
售出斤数
20
35
10
30
15
5
50
(1)、这一周超市售出的百香果单价最高的是星期 , 最高单价是元.(2)、这一周超市出售此种百香果的收益如何?(盈利或亏损的钱数)(3)、超市为了促销这种百香果,决定从下周一起推出两种促销方式:方式一:购买不超过5斤百香果,每斤12元,超出5斤的部分,每斤打8折;
方式二:每斤售价10元.
于老师决定买35斤百香果,通过计算说明用哪种方式购买更省钱.
24. 已知将一副三角板(直角三角板 和直角三角板 )的两个顶点重合于点 . (1)、如图1,将直角三角板 绕点 逆时针方向转动,当 恰好平分 时, 的度数是.(2)、如图2,当三角板 摆放在 内部时,作射线 平分 ,射线 平分 ,如果三角板 在 内绕点 任意转动, 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.(3)、当三角板 绕点 继续转动到如图3所示的位置时,作射线 平分 ,射线 平分 ,请你求出此时钝角 的度数.
(1)、如图1,将直角三角板 绕点 逆时针方向转动,当 恰好平分 时, 的度数是.(2)、如图2,当三角板 摆放在 内部时,作射线 平分 ,射线 平分 ,如果三角板 在 内绕点 任意转动, 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.(3)、当三角板 绕点 继续转动到如图3所示的位置时,作射线 平分 ,射线 平分 ,请你求出此时钝角 的度数.