河北省石家庄市正定县2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. -3的倒数是( )A、 B、 C、 D、-32. 在0,2,﹣3,﹣ 这四个数中,最小的数是( )A、0 B、2 C、﹣3 D、﹣3. 如果零上2℃记作+2℃,那么零下3℃记作()A、-3℃ B、-2℃ C、+3℃ D、+2℃4. 用量角器测量 的度数,操作正确的是( )A、
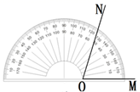 B、
B、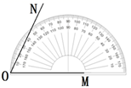 C、
C、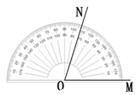 D、
D、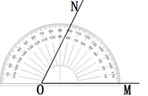 5. =( )A、 B、 C、 D、6. 将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )
5. =( )A、 B、 C、 D、6. 将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )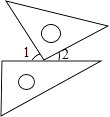 A、30°10′ B、60°10′ C、59°50′ D、60°50′7. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b﹣a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
A、30°10′ B、60°10′ C、59°50′ D、60°50′7. 点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b﹣a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )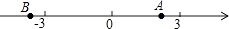 A、甲、乙 B、丙、丁 C、甲、丙 D、乙、丁8. 如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )
A、甲、乙 B、丙、丁 C、甲、丙 D、乙、丁8. 如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是( )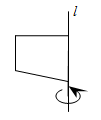 A、
A、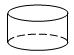 B、
B、 C、
C、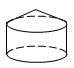 D、
D、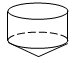 9. 已知 , 都是有理数,且 ,则 ( )A、1 B、4 C、-1 D、-410. 下列各组数中,互为相反数的有( )
9. 已知 , 都是有理数,且 ,则 ( )A、1 B、4 C、-1 D、-410. 下列各组数中,互为相反数的有( )① 和 ;② 和 ;③ 和 ;④ 和 .
A、④ B、①② C、①②③ D、①②④11. 如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数α是( )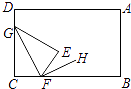 A、90°<α<180° B、0°<α<90° C、α=90° D、α随折痕GF位置的变化而变化12. 如图,用尺规作出∠OBF=∠AOB,所画痕迹 是( )
A、90°<α<180° B、0°<α<90° C、α=90° D、α随折痕GF位置的变化而变化12. 如图,用尺规作出∠OBF=∠AOB,所画痕迹 是( )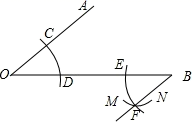 A、以点B为圆心,OD为半径的弧 B、以点C为圆心,DC为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DC为半径的弧13. 如图,将一副三角板的直角顶点重合摆放在在桌面上,下列各组角一定能互补的是( )
A、以点B为圆心,OD为半径的弧 B、以点C为圆心,DC为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DC为半径的弧13. 如图,将一副三角板的直角顶点重合摆放在在桌面上,下列各组角一定能互补的是( )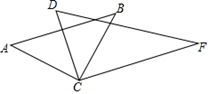 A、∠BCD和∠ACF B、∠ACD和∠ACF C、∠ACB和∠DCB D、∠BCF和∠ACF14. 摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟,若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,3号车厢才会运行到最高点?( )
A、∠BCD和∠ACF B、∠ACD和∠ACF C、∠ACB和∠DCB D、∠BCF和∠ACF14. 摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟,若图2表示21号车厢运行到最高点的情形,则此时经过多少分钟后,3号车厢才会运行到最高点?( )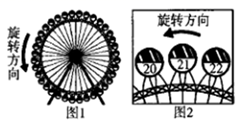 A、14分钟 B、20分钟 C、15分钟 D、 分钟
A、14分钟 B、20分钟 C、15分钟 D、 分钟二、填空题
-
15. 、 两地之间弯曲的公路改直,能够缩短路程,其根据的道理是.16. 已知线段 , , , , 三点在同一直线上,那么 等于.17. 已知 、 互为倒数, 、 互为相反数,则 .18. 观察下列等式
, , ,
将以上三个等式两边分别相加得:
.
(1)、猜想并写出: ;(2)、直接写出下列各式的计算结果:;
(3)、探究并计算:.
三、解答题
-
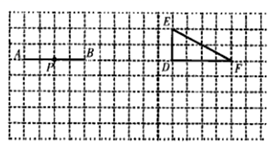
19. 计算(1)、(2)、(3)、(4)、20. 如图,网格图中每一小格的边长为1个单位长度.请分别画出线段 绕中点 和三角形 绕点 ,按顺时针方向旋转 后的图形线段 ,三角形 .
 21. 在一条不完整的数轴上从左到右有点 , , ,其中 , ,如图所示,设点 , , 所对应数的和是p.
21. 在一条不完整的数轴上从左到右有点 , , ,其中 , ,如图所示,设点 , , 所对应数的和是p.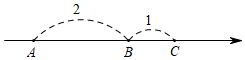 (1)、若以 为原点,写出点 , 所对应的数,并计算p的值;若以 为原点,p又是多少?(2)、若原点 在图中数轴上点 的右边,且 ,求p.22. 如图,点 为线段 上一点,点 为 的中点,且 , .
(1)、若以 为原点,写出点 , 所对应的数,并计算p的值;若以 为原点,p又是多少?(2)、若原点 在图中数轴上点 的右边,且 ,求p.22. 如图,点 为线段 上一点,点 为 的中点,且 , . (1)、图中共有多少条线段?(2)、求 的长.(3)、若点 在直线 上,且 ,求 的长.23. 黄桃是我县南楼乡东里双村的一大特产,现有20筐黄桃,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
(1)、图中共有多少条线段?(2)、求 的长.(3)、若点 在直线 上,且 ,求 的长.23. 黄桃是我县南楼乡东里双村的一大特产,现有20筐黄桃,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:与标准质量的差值
(单位:千克)
-3
-2
-1.5
0
1
2.5
筐数
1
4
2
3
2
8
(1)、20筐黄桃中,与标准质量差值为-2千克的有筐,最重的一筐重千克,最轻的一筐重千克,最重的一筐比最轻的一筐重千克;(2)、与标准重量比较,20筐黄桃总计超过多少千克?(3)、若黄桃每千克售价3元,则出售这20筐黄桃可卖多少元?24. 下列各小题中,都有OE平分∠AOC , OF平分∠BOC .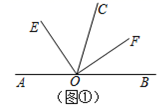
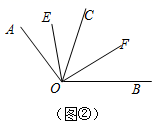
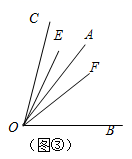 (1)、如图①,若点A、O、B在一条直线上,∠EOF= ;(2)、如图②,若点A、O、B不在一条直线上,∠AOB=140°,则∠EOF=;(3)、由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB的数量关系是∠EOF=;(4)、如图③,若OA在∠BOC的内部,∠AOB和∠EOF还存在上述的数量关系吗?请简单说明理由;
(1)、如图①,若点A、O、B在一条直线上,∠EOF= ;(2)、如图②,若点A、O、B不在一条直线上,∠AOB=140°,则∠EOF=;(3)、由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB的数量关系是∠EOF=;(4)、如图③,若OA在∠BOC的内部,∠AOB和∠EOF还存在上述的数量关系吗?请简单说明理由;