河北省唐山市滦南县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 的值是( )A、 B、 C、 D、
-
2. 为了解我校初二年级800名学生的体重情况,从中抽取了80名学生的体重,就这个问题来说,下面说法正确的是( )A、800名学生的体重是总体 B、800名学生是总体 C、每个学生是个体 D、80名学生是所抽取的一个样本
-
3. 若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为( )A、3:4 B、4:3 C、 :2 D、2:
-
4. 某中学随机调查了15名学生,了解他们一周在校参加体育锻炼的时间,列表如下:
锻炼时间/h
5
6
7
8
人数
2
6
5
2
则这 15 名学生一周在校参加体育锻炼时间的中位数和众数分别为( )
A、6 h , 6 h B、7 h , 7 h C、7 h , 6 h D、6 h , 7 h -
5. 已知 ,则 的值为( )A、 B、 C、 D、
-
6. 甲、乙、丙、丁四位选手各进行了10次射击,射击成绩的平均数和方差如下表:
选手
甲
乙
丙
丁
平均数(环)
9.0
9.0
9.0
9.0
方差
0.25
1.00
2.50
3.00
则成绩发挥最不稳定的是( )
A、甲 B、乙 C、丙 D、丁 -
7. 关于x的一元二次方程(2-a)x2+x+a2-4=0的一个根为0,则a的值为( )A、2 B、0 C、2或-2 D、-2
-
8. 某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95,90,85.则小桐这学期的体育成绩是( )A、88.5 B、86.5 C、90 D、90.5
-
9. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根
-
10. 如图,已知 , , , 的长为( )
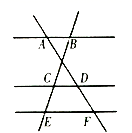 A、2 B、4 C、3 D、5
A、2 B、4 C、3 D、5 -
11. 下列一元二次方程中,两个实数根之和为2的是( )A、2x2+x﹣2=0 B、x2+2x﹣2=0 C、2x2﹣x﹣1=0 D、x2﹣2x﹣2=0
-
12. 已知α为锐角,tanα= ,则sinα=( )A、 B、 C、 D、
-
13. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
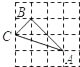 A、
A、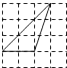 B、
B、 C、
C、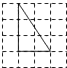 D、
D、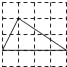
-
14. 一个不透明的袋子中有红球、白球共20个这些球除颜色外都相同将袋子中的球搅匀后,从中随意摸出1个球,记下颜色后放回,不断重复这个过程,共摸了100次,其中有30次摸到红球,由此可以估计袋子中红球的个数约为( )A、12 B、10 C、8 D、6
-
15. 如图,点P(8,6)在△ABC的边AC上,以原点O为位似中心,在第一象限内将△ABC缩小到原来的 ,得到△A′B′C′,点P在A′C′上的对应点P′的的坐标为( )
 A、(4,3) B、(3,4) C、(5,3) D、(4,4)
A、(4,3) B、(3,4) C、(5,3) D、(4,4) -
16.
如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题
-
17. 若α、β是一元二次方程x2+2x﹣3=0的两个不相等的根,则α2﹣2β的值是.
-
18. 如图,某海监船以20km/h的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为km .

-
19. 如图,等腰△ABC中,AB=AC , ∠A=36°,作底角∠ABC的平分线BD交AC于点D , 易得等腰△BCD , 作等腰△BCD底角∠BCD的平分线CE , 交BD于点E , 得等腰△CDE , 再作等腰△CDE底角∠CDE的平分线DF , 交于CE于点F , …,若已知AB=b , BC=a , 记△ABC为第一个等腰三角形,△BCD为第二个等腰三角形…,则 的值为;第n个等腰三角形的底边长为 . (含有b的代数式表示)

三、解答题
-
20. 如图,某校宣传栏BC后面12米处种有一排与宣传栏平行的若干棵树,即BC∥ED , 且相邻两棵树的间隔为2米,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知AF⊥BC , AF=3米,BC=10米,求该宣传栏后DE处共有多少棵树?(不计宣传栏的厚度).

-
21. 在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
 (1)、本次调查的样本容量是 , 这组数据的众数为元;(2)、求这组数据的平均数;(3)、该校共有 学生参与捐款,请你估计该校学生的捐款总数.
(1)、本次调查的样本容量是 , 这组数据的众数为元;(2)、求这组数据的平均数;(3)、该校共有 学生参与捐款,请你估计该校学生的捐款总数. -
22. 如图,水库大坝的横截面是梯形,坝顶宽5米,CD的长为20 米,斜坡AB的坡度i=1:2.5(i为坡比即BE:AE),斜坡CD的坡度i=1:2(i为坡比即CF:FD),求坝底宽AD的长.

-
23. 已知关于x的一元二次方程mx2﹣2x+2﹣m=0.(1)、证明:不论m为何值时,方程总有实数根;(2)、当m为何整数时,方程有两个不相等的整数根.
-
24. 如图,在 中,过点 作 ,垂足为 ,连接 , 为 上一点,且 .
 (1)、试说明: ∽ ;(2)、若 , , ,求 的长.
(1)、试说明: ∽ ;(2)、若 , , ,求 的长. -
25. 慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
 (1)、求小亮与塔底中心的距离BD;(用含a的式子表示)(2)、若小亮与小琴相距52米,求慈氏塔的高度AB.
(1)、求小亮与塔底中心的距离BD;(用含a的式子表示)(2)、若小亮与小琴相距52米,求慈氏塔的高度AB. -
26. 阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想 转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
 (1)、问题:方程x3+x2-2x=0的解是x1=0,x2= , x3=;(2)、拓展:用“转化”思想求方程 的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
(1)、问题:方程x3+x2-2x=0的解是x1=0,x2= , x3=;(2)、拓展:用“转化”思想求方程 的解;(3)、应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
