河北省唐山市丰润区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 下列图形中是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若关于x的方程(a+1)x2+2x﹣1=0是一元二次方程,则a的取值范围是( )A、a≠﹣1 B、a>﹣1 C、a<﹣1 D、a≠03. 方程x2=2x的解是( )A、x1=﹣2,x2=0 B、x1= ,x2=0 C、x1=1,x2=2 D、x1=2,x2=04. 抛物线y=x2+1的对称轴是( )A、直线x=﹣1 B、直线x=1 C、直线x=0 D、直线y=15. 把方程x2﹣12x+33=0化成(x+m)2=n的形式,则m、n的值是( )A、6,3 B、﹣6,﹣3 C、﹣6,3 D、6,﹣36. 在平面直角坐标系中,有A(2,-1)、B(-1,-2)、C(2,1)、D(-2,1)四点.其中,关于原点对称的两点为( )A、点A和点B B、点B和点C C、点C和点D D、点D和点A7. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+5 C、y= (x﹣8)2+3 D、y= (x﹣4)2+38. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
2. 若关于x的方程(a+1)x2+2x﹣1=0是一元二次方程,则a的取值范围是( )A、a≠﹣1 B、a>﹣1 C、a<﹣1 D、a≠03. 方程x2=2x的解是( )A、x1=﹣2,x2=0 B、x1= ,x2=0 C、x1=1,x2=2 D、x1=2,x2=04. 抛物线y=x2+1的对称轴是( )A、直线x=﹣1 B、直线x=1 C、直线x=0 D、直线y=15. 把方程x2﹣12x+33=0化成(x+m)2=n的形式,则m、n的值是( )A、6,3 B、﹣6,﹣3 C、﹣6,3 D、6,﹣36. 在平面直角坐标系中,有A(2,-1)、B(-1,-2)、C(2,1)、D(-2,1)四点.其中,关于原点对称的两点为( )A、点A和点B B、点B和点C C、点C和点D D、点D和点A7. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+5 C、y= (x﹣8)2+3 D、y= (x﹣4)2+38. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )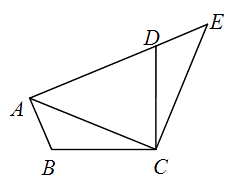 A、55° B、60° C、65° D、70°9. 下列对二次函数y=x2﹣x的图象的描述,正确的有( )A、开口向下 B、对称轴是y轴 C、经过原点 D、在对称轴右侧,抛物线从左到右下降10. 某种药品经过了两次降价,从每盒54元降到每盒42元 若平均每次降低的百分率都为x,则根据题意,可得方程A、 B、 C、 D、11. 菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )A、16 B、12 C、16或12 D、2412. 二次函数 的图象大致是( )A、
A、55° B、60° C、65° D、70°9. 下列对二次函数y=x2﹣x的图象的描述,正确的有( )A、开口向下 B、对称轴是y轴 C、经过原点 D、在对称轴右侧,抛物线从左到右下降10. 某种药品经过了两次降价,从每盒54元降到每盒42元 若平均每次降低的百分率都为x,则根据题意,可得方程A、 B、 C、 D、11. 菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )A、16 B、12 C、16或12 D、2412. 二次函数 的图象大致是( )A、 B、
B、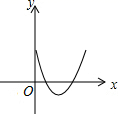 C、
C、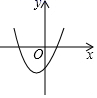 D、
D、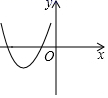 13. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则( )
13. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则( )①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
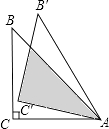
14. 点A(﹣3,m)和点B(n,2)关于原点对称,则m+n= .15. 已知一元二次方程x2+2x﹣1=0的两实数根为x1 , x2 , 则x1x2的值为 .16. 已知二次函数的图象经过点(1,3)和(3,3),则此函数图象的对称轴与x轴的交点坐标是 .17. 若x=﹣2是关于x的一元二次方程x2+ ax﹣a2=0的一个根,则a的值为 .18. 二次函数y=﹣x2﹣2x+3的最大值是 .19. 如果关于x的一元二次方程2x(kx-4)-x2+6=0没有实数根,那么k的最小整数值是.20. 如图,等腰Rt△ABC中,∠C=90°,BC=6cm , 将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是cm2 .
三、解答题
-
21.(1)、解方程:x2+4x﹣7=0(2)、解方程:3x(x﹣1)=2x﹣222. 在如图网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
 (1)、试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;(2)、若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并直接写出A、C两点的坐标;(3)、根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2 , 并直接写出点A2、B2、C2的坐标.23. 已知m是方程x2﹣3x+1=0的一个根,求(m﹣3)2+(m+2)(m﹣2)的值.24. 如图,在平面直角坐标系中,过抛物线 的顶点A作x轴的平行线,交抛物线y=x2+1于点B , 点B在第一象限.
(1)、试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;(2)、若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并直接写出A、C两点的坐标;(3)、根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2 , 并直接写出点A2、B2、C2的坐标.23. 已知m是方程x2﹣3x+1=0的一个根,求(m﹣3)2+(m+2)(m﹣2)的值.24. 如图,在平面直角坐标系中,过抛物线 的顶点A作x轴的平行线,交抛物线y=x2+1于点B , 点B在第一象限. (1)、求点A的坐标;(2)、点P为x轴上任意一点,连结AP、BP , 求△ABP的面积.25. 如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D'.设旋转角为α,此时点B′恰好落在边AD上,连接B'B .
(1)、求点A的坐标;(2)、点P为x轴上任意一点,连结AP、BP , 求△ABP的面积.25. 如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D'.设旋转角为α,此时点B′恰好落在边AD上,连接B'B . (1)、当B'恰好是AD中点时,此时α=;(2)、若∠AB'B=75°,求旋转角α及AB的长.26. 双十一期间,某百货商场打算对某商品进行一次促销活动,该商品的进价为每件20元.在之前的销售过程中发现,当每件售价定为30元时,每月销售量为500件,若售价每提高1元,每月的销售量将减少10件.(1)、设该商品售价提高x元时,每月获得的利润为y元,求y关于x的函数解析式;(2)、如果商场想要获得的月利润为8000元,则该商品的销售单价应定为每件多少元?(3)、若有关物价部门规定,该商品的销售单价不得高于其进价的两倍,则此时商场获得的最大月利润是多少?27. 如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)、当B'恰好是AD中点时,此时α=;(2)、若∠AB'B=75°,求旋转角α及AB的长.26. 双十一期间,某百货商场打算对某商品进行一次促销活动,该商品的进价为每件20元.在之前的销售过程中发现,当每件售价定为30元时,每月销售量为500件,若售价每提高1元,每月的销售量将减少10件.(1)、设该商品售价提高x元时,每月获得的利润为y元,求y关于x的函数解析式;(2)、如果商场想要获得的月利润为8000元,则该商品的销售单价应定为每件多少元?(3)、若有关物价部门规定,该商品的销售单价不得高于其进价的两倍,则此时商场获得的最大月利润是多少?27. 如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.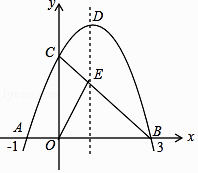 (1)、求此抛物线的解析式;(2)、求点C和点D的坐标;(3)、若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标.
(1)、求此抛物线的解析式;(2)、求点C和点D的坐标;(3)、若点P在第一象限内的抛物线上,且S△ABP=4S△COE , 求P点坐标.