河北省唐山市丰南区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 一元二次方程 的解是( )A、 B、 C、 D、2. 已知二次函数y=(2﹣a) ,在其图象对称轴的左侧,y随x的增大而减小,则a的值为( )A、 B、± C、﹣ D、03. 下面四个手机应用图标中是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 4. 用配方法解下列方程时,配方有错误的是( )A、 化为 B、 化为 C、 化为 D、 化为5. 将抛物线 向上平移 个单位后得到的抛物线恰好与 轴有一个交点,则a的值为( )A、-1 B、1 C、-2 D、26. 若一元二次方程 的两个实数根分别是 ,则 ( )A、-1 B、1 C、3 D、-47. 点P1(﹣1, ),P2(3, ),P3(5, )均在二次函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,在 中, .将 绕点 按逆时针方向旋转 得到 ,点 在边 上,则 的大小为( )
4. 用配方法解下列方程时,配方有错误的是( )A、 化为 B、 化为 C、 化为 D、 化为5. 将抛物线 向上平移 个单位后得到的抛物线恰好与 轴有一个交点,则a的值为( )A、-1 B、1 C、-2 D、26. 若一元二次方程 的两个实数根分别是 ,则 ( )A、-1 B、1 C、3 D、-47. 点P1(﹣1, ),P2(3, ),P3(5, )均在二次函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,在 中, .将 绕点 按逆时针方向旋转 得到 ,点 在边 上,则 的大小为( ) A、 B、 C、 D、9. 下列是抛物线y=﹣2x2﹣3x+1的图象大致是( )A、
A、 B、 C、 D、9. 下列是抛物线y=﹣2x2﹣3x+1的图象大致是( )A、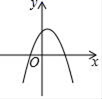 B、
B、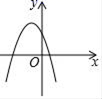 C、
C、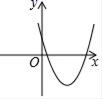 D、
D、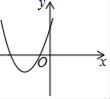 10. 关于 的一元二次方程 总有实数根,则 的取值范围( )A、 且 B、 且 C、 D、 且11. 有 人患了流感,经过两轮传染后共有 人患了流感,设每轮传染中平均一个人传染了 人,则 的为( )A、5 B、6 C、7 D、812. 二次函数 的图象如图所示,则下列判断中错误的是( )
10. 关于 的一元二次方程 总有实数根,则 的取值范围( )A、 且 B、 且 C、 D、 且11. 有 人患了流感,经过两轮传染后共有 人患了流感,设每轮传染中平均一个人传染了 人,则 的为( )A、5 B、6 C、7 D、812. 二次函数 的图象如图所示,则下列判断中错误的是( )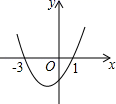 A、图象的对称轴是直线 B、当 时, 随 的增大而减小 C、当 时, D、一元二次方程 的两个根是13. 如图,在 中, ,将 绕点 逆时针旋转,使点 落在线段 上的点 处,点 落在点 处,则 两点间的距离为( )
A、图象的对称轴是直线 B、当 时, 随 的增大而减小 C、当 时, D、一元二次方程 的两个根是13. 如图,在 中, ,将 绕点 逆时针旋转,使点 落在线段 上的点 处,点 落在点 处,则 两点间的距离为( )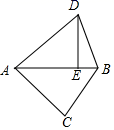 A、 B、 C、3 D、14. 如图,在 中, ,点 从点 开始沿 边向点 以 的速度匀速移动,同时另一点 由 点开始以 的速度沿着射线 匀速移动,当 的面积等于 时运动时间为( )
A、 B、 C、3 D、14. 如图,在 中, ,点 从点 开始沿 边向点 以 的速度匀速移动,同时另一点 由 点开始以 的速度沿着射线 匀速移动,当 的面积等于 时运动时间为( )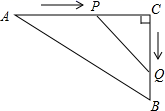 A、10秒 B、5秒 C、20秒 D、5秒或20秒15. 已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=-t2+24t+1.则下列说法中正确的是( )A、点火后9 s和点火后13 s的升空高度相同 B、点火后24 s火箭落于地面 C、点火后10 s的升空高度为139 m D、火箭升空的最大高度为145 m16. 如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1 , 将C1以y铀为对称轴作轴对称得到C2 , C2与x轴交于点B,若直线y=x+m与C1 , C2共有3个不同的交点,则m的取值范围是( )
A、10秒 B、5秒 C、20秒 D、5秒或20秒15. 已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h=-t2+24t+1.则下列说法中正确的是( )A、点火后9 s和点火后13 s的升空高度相同 B、点火后24 s火箭落于地面 C、点火后10 s的升空高度为139 m D、火箭升空的最大高度为145 m16. 如图,抛物线y=﹣2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1 , 将C1以y铀为对称轴作轴对称得到C2 , C2与x轴交于点B,若直线y=x+m与C1 , C2共有3个不同的交点,则m的取值范围是( )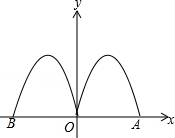 A、0<m< B、 <m< C、0<m< D、m< 或m<
A、0<m< B、 <m< C、0<m< D、m< 或m<二、填空题
-
17. 方程 化为一般式为 .18. 二次函数 的图象如图所示,以下结论:① ;② ;③ ;④其顶点坐标为 ;⑤当 时, 随 的增大而减小;⑥ 中,正确的有(只填序号)
 19. 如图,在长为 米,宽为 米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上小草.要使草坪的面积为 平方米,则道路的宽为米.
19. 如图,在长为 米,宽为 米的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上小草.要使草坪的面积为 平方米,则道路的宽为米.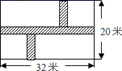 20. 如图所示,点阵 的层数用 表示,点数总和用 表示, 当 时,则 . 层点阵的点数 .
20. 如图所示,点阵 的层数用 表示,点数总和用 表示, 当 时,则 . 层点阵的点数 .
三、解答题
-
21. 二次函数(1)、写出函数图象的开口方向、顶点坐标和对称轴.(2)、判断点 是否在该函数图象上,并说明理由.(3)、求出以该抛物线与两坐标轴的交点为顶点的三角形的面积.22. 如图,
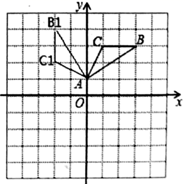 (1)、 绕点逆时针旋转度得到 ;(2)、画出 绕原点 顺时针旋转 的 ,直接写出点 坐标;若 内一点 在 的对应.,点为 ,则 的坐标为_ _.(用含 的式子表示)(3)、在 轴上描出点 ,使 最小,此时 .23. 如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.
(1)、 绕点逆时针旋转度得到 ;(2)、画出 绕原点 顺时针旋转 的 ,直接写出点 坐标;若 内一点 在 的对应.,点为 ,则 的坐标为_ _.(用含 的式子表示)(3)、在 轴上描出点 ,使 最小,此时 .23. 如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.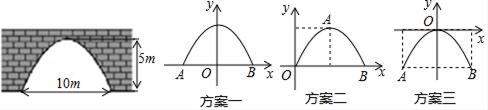 (1)、经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是(填方案一,方案二,或方案三),则B点坐标是 , 求出你所选方案中的抛物线的表达式;(2)、因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.24. 如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC , 连接OD , OA .
(1)、经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是(填方案一,方案二,或方案三),则B点坐标是 , 求出你所选方案中的抛物线的表达式;(2)、因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.24. 如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC , 连接OD , OA .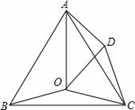 (1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.25. 某商场一种商品的进价为每件30元,售价为每件50元.每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)、若该商品连续两次下调相同的百分率后售价降至每件40.5元,求两次下降的百分率;(2)、经调查,若该商品每降价2元,每天可多销售16件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?26. 如图,二次函数 的图象与 轴交于 两点,与 轴交于点 .点 在函数图象上, 轴,且 ,直线 是抛物线的对称轴, 是抛物线的顶点.
(1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.25. 某商场一种商品的进价为每件30元,售价为每件50元.每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)、若该商品连续两次下调相同的百分率后售价降至每件40.5元,求两次下降的百分率;(2)、经调查,若该商品每降价2元,每天可多销售16件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?26. 如图,二次函数 的图象与 轴交于 两点,与 轴交于点 .点 在函数图象上, 轴,且 ,直线 是抛物线的对称轴, 是抛物线的顶点.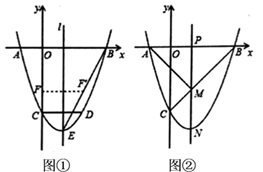 (1)、求 的值;(2)、如图①,连接 , 线段 上的点 关于直线 的对称点F'恰好在线段BE上,求点 的坐标;(3)、如图②,动点 在线段 上,过点 作 轴的垂线分别与 交于点 ,与抛物线交于点 .试问:直线 右侧的抛物线上是否存在点 ,使得 与 的面积相等,且线段 的长度最小?如果存在,求出点 的坐标;如果不存在,说明理由.
(1)、求 的值;(2)、如图①,连接 , 线段 上的点 关于直线 的对称点F'恰好在线段BE上,求点 的坐标;(3)、如图②,动点 在线段 上,过点 作 轴的垂线分别与 交于点 ,与抛物线交于点 .试问:直线 右侧的抛物线上是否存在点 ,使得 与 的面积相等,且线段 的长度最小?如果存在,求出点 的坐标;如果不存在,说明理由.