河北省石家庄市正定县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 小明在最近五次数学测试中,前四次的成绩分别是96分、98分、94分和92分,第五次因病只得了45分,则代表小明数学学习水平的数据是这五次数学成绩的( )
A、平均数 B、方差 C、众数 D、中位数2. 若关于 的方程 是一元二次方程,则 的值不可能是( )A、2 B、 C、0 D、33. 已知线段 , ,线段 是 , 的比例中项,则 等于( )A、36 B、6 C、-6 D、6或-64. 在 中, ,如果 ,那么 的值是( )A、1 B、 C、 D、5. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A、甲 B、乙 C、丙 D、丁6. 用配方法解方程 ,配方后所得方程是( )A、 B、 C、 D、7. 在Rt△ABC中,∠C=90°,各边都扩大2倍,则锐角A的锐角三角函数值( )A、扩大2倍 B、缩小 C、不变 D、无法确定8. 如图,已知直线 , , 分别交直线 于点A,B,C,交直线l,于点D,E,F,且 ,若 , , ,则DE的长为( ) A、5 B、6 C、7 D、89. 若 , 是一个三角形的两个锐角,且满足 ,则此三角形为( )A、等腰三角形 B、直角三角形 C、等边三角形 D、等腰直角三角形10. 某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、25% C、50% D、62.5%11. 三角形的两边长分别为4和5,第三边的长是方程 的根,则三角形的周长是( )A、19 B、11或19 C、13 D、1112. 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表如图,比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A、5 B、6 C、7 D、89. 若 , 是一个三角形的两个锐角,且满足 ,则此三角形为( )A、等腰三角形 B、直角三角形 C、等边三角形 D、等腰直角三角形10. 某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )A、20% B、25% C、50% D、62.5%11. 三角形的两边长分别为4和5,第三边的长是方程 的根,则三角形的周长是( )A、19 B、11或19 C、13 D、1112. 甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表如图,比较5月份两组家庭用水量的中位数,下列说法正确的是( )甲组12户家庭用水量统计表
用水量(吨)
4
5
6
9
户数
4
5
2
1
 A、甲组比乙组大 B、甲、乙两组相同 C、乙组比甲组大 D、无法判断13. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A、甲组比乙组大 B、甲、乙两组相同 C、乙组比甲组大 D、无法判断13. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )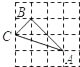 A、
A、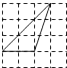 B、
B、 C、
C、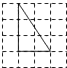 D、
D、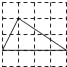 14. 如图,在△ABC中,点D,E分别是边AC,AB的中点,BD与CE交于点O,连接DE.下列结论:① ;② ;③ ;④ .其中正确的个数有( )
14. 如图,在△ABC中,点D,E分别是边AC,AB的中点,BD与CE交于点O,连接DE.下列结论:① ;② ;③ ;④ .其中正确的个数有( )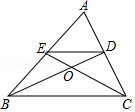 A、1个 B、2个 C、3个 D、4个15. 如图,已知 , , , 为 边上一点,且 , 为 边上一点(不与 、 重合),若 与 相似,则
A、1个 B、2个 C、3个 D、4个15. 如图,已知 , , , 为 边上一点,且 , 为 边上一点(不与 、 重合),若 与 相似,则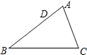 A、2 B、 C、3或 D、3或16. 小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=3,解出其中一个根是x=﹣1.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有一个根是x=﹣1 D、有两个相等的实数根
A、2 B、 C、3或 D、3或16. 小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=3,解出其中一个根是x=﹣1.他核对时发现所抄的c比原方程的c值小2.则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有一个根是x=﹣1 D、有两个相等的实数根二、填空题
-
17. 若 ( , , 均不为0),则 的值为18. 已知m是方程 的一个根,则代数式 .19. 如图,在平行四边形 中, , , , 是 上的一点,且 ,则 的长为
 20. 如图,小红作出了边长为1的第1个正三角形 ,算出了正 的面积,然后分别取 三边的中点 ,作出了第二个正三角形 ,算出第2个正 的面积,用同样的方法作出了第3个正 ,算出第3个正 的面积,依此方法作下去,由此可得第 个作出的正 的面积是
20. 如图,小红作出了边长为1的第1个正三角形 ,算出了正 的面积,然后分别取 三边的中点 ,作出了第二个正三角形 ,算出第2个正 的面积,用同样的方法作出了第3个正 ,算出第3个正 的面积,依此方法作下去,由此可得第 个作出的正 的面积是
三、解答题
-
21.(1)、解方程(2)、计算:22. 某班级从甲、乙两位同学中选派一人参加知识竞赛,老师对他们的五次模拟成绩(单位:分)进行了整理,并计算出甲成绩的平均数是80分,甲、乙成绩的方差分别是320,40,但绘制的统计图表尚不完整.
甲、乙两人模拟成绩统计表
第一次
第二次
第三次
第四次
第五次
甲成绩
90
100
90
50
乙成绩
80
70
80
90
80
甲、乙两人模拟成绩折线图

根据以上信息,请你解答下列问题:
(1)、a=(2)、请完成图中表示甲成绩变化情况的折线;(3)、求乙成绩的平均数;(4)、从平均数和方差的角度分析,谁将被选中.23. 如图,△ABC中,A(﹣4,4),B(﹣4,﹣2),C(﹣2,2). (1)、请画出将△ABC向右平移8个单位长度后的△A1BlC1;(2)、求出∠A1BlC1的余弦值;(3)、以O为位似中心,将△A1BlC1缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 .24. 油井A位于油库P南偏东75°方向,主输油管道AP=12km,一新建油井B位于点P的北偏东75°方向,且位于点A的北偏西15°方向.(1)、求∠PBA;(2)、求A,B间的距离;(3)、要在AP上选择一个支管道连接点C,使从点B到点C处的支输油管道最短,求这时BC的长.(结果保留根号)25. 某水果店销售一种水果的成本价是5元/千克,在销售中发现,当这种水果的价格定为7元/千克时,每天可以卖出160千克,在此基础上,这种水果的单价每提高1元/千克,该水果店每天就会少卖出20千克,设这种水果的单价为 元( ),(1)、请用含 的代数式表示:每千克水果的利润元及每天的销售量千克.(2)、若该水果店一天销售这种水果所获得的利润是420元,为了让利于顾客,单价应定为多少元?26. 阅读下面材料:
(1)、请画出将△ABC向右平移8个单位长度后的△A1BlC1;(2)、求出∠A1BlC1的余弦值;(3)、以O为位似中心,将△A1BlC1缩小为原来的 ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 .24. 油井A位于油库P南偏东75°方向,主输油管道AP=12km,一新建油井B位于点P的北偏东75°方向,且位于点A的北偏西15°方向.(1)、求∠PBA;(2)、求A,B间的距离;(3)、要在AP上选择一个支管道连接点C,使从点B到点C处的支输油管道最短,求这时BC的长.(结果保留根号)25. 某水果店销售一种水果的成本价是5元/千克,在销售中发现,当这种水果的价格定为7元/千克时,每天可以卖出160千克,在此基础上,这种水果的单价每提高1元/千克,该水果店每天就会少卖出20千克,设这种水果的单价为 元( ),(1)、请用含 的代数式表示:每千克水果的利润元及每天的销售量千克.(2)、若该水果店一天销售这种水果所获得的利润是420元,为了让利于顾客,单价应定为多少元?26. 阅读下面材料:小腾遇到这样一个问题:如图1,在 中,点 在线段 上. , , , .求 的长.
小腾发现,过点 作 ,交 的延长线于点 ,通过构造 ,经过推理和计算能够使问题得到解决(如图2).
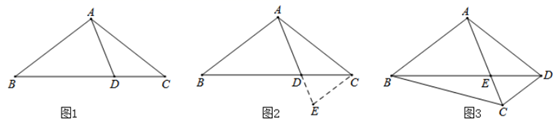 (1)、发现: 的度数为 , 的长为(2)、探究:参考小腾思考问题的方法,解决问题:
(1)、发现: 的度数为 , 的长为(2)、探究:参考小腾思考问题的方法,解决问题:如图3,在四边形 中, , , , 与 交于点 , , ,求 , 的长.