河北省石家庄市新乐市2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-25 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程x²＝4的解是（）

A、x＝﹣2 B、x＝2 C、x＝± $\sqrt{2}$ D、x＝±2

查看试题解析
2. 下列对一元二次方程x²+x﹣3=0根的情况的判断，正确的是（）

A、有两个不相等实数根 B、有两个相等实数根 C、有且只有一个实数根 D、没有实数根

查看试题解析
3. 某同学将自己7次体育测试成绩（单位：分）绘制成折线统计图，则该同学7次测试成绩的众数和中位数分别是（）

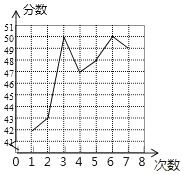A、50和48 B、50和47 C、48和48 D、48和43

查看试题解析
4.
如图，已知直线a∥b∥c，直线m，n与a，b，c分别交于点A，C，E，B，D，F，若AC=4，CE=6，BD=3，则DF的值是（　　）

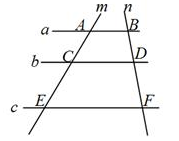A、4 B、4.5 C、5 D、5.5

查看试题解析
5. 把一元二次方程x²﹣6x+1＝0配方成（x+m）²＝n的形式，正确的是（　　）

A、（x+3）²＝10 B、（x﹣3）²＝10 C、（x+3）²＝8 D、（x﹣3）²＝8

查看试题解析
6. 下列各组图形必相似的是（　　）

A、任意两个等腰三角形 B、有两边对应成比例，且有一个角对应相等的两三角形 C、两边为4和5的直角三角形与两边为8和10的直角三角形 D、两边及其中一边上的中线对应成比例的两三角形

查看试题解析
7. 通过统计甲、乙、丙、丁四名同学某学期的四次数学测试成绩，得到甲、乙、丙、丁三明同学四次数学测试成绩的方差分别为S_甲²＝17，S_乙²＝36，S_丙²＝14，丁同学四次数学测试成绩（单位：分）.如下表：

第一次

第二次

第三次

第四次

丁同学

80

80

90

90

则这四名同学四次数学测试成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 下列方程中，有实数根的是（）

A、 $\sqrt{1 + x} = - 1$ B、 $\sqrt{x - 1} = - x$ C、x³+3＝0 D、x⁴+4＝0

查看试题解析
9. 如图，△ABC中，点D在线段AB上，且△ABC∽△ACD，则下列结论一定正确的是（）

A、AC²=AB·AD B、AC²=BC·AD C、AC·CD=AB·AD D、AC·CD=CD·BD

查看试题解析
10. 某经济技术开发区今年一月份工业产值达50亿元，且第一季度的产值为175亿元.若设平均每月的增长率为x，根据题意可列方程为（）

A、50(1＋x)²＝175 B、50＋50(1＋x)²＝175 C、50(1＋x)＋50(1＋x)²＝175 D、50＋50(1＋x)＋50(1＋x)²＝175

查看试题解析
11. 已知一元二次方程 $x^{2} - 3 x - 1 = 0$ 的两个实数根分别是 x₁ 、 x₂ 则 x₁² x₂ + x₁ x₂² 的值为（）

A、-6 B、- 3 C、3 D、6

查看试题解析
12. 如图，在塔AB前的平地上选择一点C ，测出看塔顶的仰角为30°，从C点向塔底走100米到达D点，测出看塔顶的仰角为45°，则塔AB的高为（）

A、50 $\sqrt{3}$ 米 B、100 $\sqrt{3}$ 米 C、50（ $\sqrt{3}$ +1）米 D、50（ $\sqrt{3}$ ﹣1）米

查看试题解析
13. 今年“国庆节”和“中秋节”双节期间，某微信群规定，群内的每个人都要发一个红包，并保证群内其他人都能抢到且自己不能抢自己发的红包，若此次抢红包活动，群内所有人共收到90个红包，则该群一共有（）

A、9人 B、10人 C、11人 D、12人

查看试题解析
14. 如图，若将图 $1$ 正方形剪成四块，恰能拼成图 $2$ 的矩形，设 $a = 1$ ，则 $b$ 的值为（）

A、 $\frac{\sqrt{5} + 1}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\sqrt{5} + 1$ D、 $\sqrt{5} - 1$

查看试题解析
15. sin58°、cos58°、cos28°的大小关系是（）

A、cos28°＜cos58°＜sin58° B、sin58°＜cos28°＜cos58° C、cos58°＜sin58°＜cos28° D、sin58°＜cos58°＜cos28°

查看试题解析
16. 如图：一个三角点阵，从上向下有无数多行，其中第一行 1个点，第二行2个点 ……第 $n$ 行有 $n$ 个点……，若10 是前4行之和，则465是前（）行之和.

A、20 B、25 C、28 D、30

查看试题解析

二、填空题

17. 设a、b是方程x²+x-2020=0的两个不等实根，则a²+2a+b的值是.

查看试题解析
18. 样本数据3，6，a,4，2的平均数是5，则这个样本的方差是

查看试题解析
19. 如图，n个边长为1的相邻正方形的一边均在同一直线上，点M₁ ， M₂ ， M₃ ， …M_n分别为边B₁B₂ ， B₂B₃ ， B₃B₄ ， …，B_nB_n+1的中点，△B₁C₁M₁的面积为S₁ ， △B₂C₂M₂的面积为S₂ ， …△B_n∁_nM_n的面积为S_n ，则S_n＝.（用含n的式子表示）

查看试题解析

三、解答题

20. 解方程

(1)、x²+2x﹣3=0

(2)、3x（x﹣2）=2（2﹣x）

查看试题解析
21. 某快餐店共有10名员工，所有员工工资的情况如下表：
人员
店长
厨师甲
厨师乙
会计
服务员甲
服务员乙
勤杂工
人数
1
1
1
1
1
3
2
工资额
20000
7000
4000
2500
2200
1800
1200
请解答下列问题：

(1)、餐厅所有员工的平均工资是；所有员工工资的中位数是．

(2)、用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当？

(3)、去掉店长和厨师甲的工资后，其他员工的平均工资是多少？它是否也能反映该快餐店员工工资的一般水平？

查看试题解析
22. 某条道路上通行车辆限速60千米/时，道路的AB段为监测区，监测点P到AB的距离PH为50米（如图）．已知点P在点A的北偏东45°方向上，且在点B的北偏西60°方向上，点B在点A的北偏东75°方向上，那么车辆通过AB段的时间在多少秒以内，可认定为超速？（参考数据： $\sqrt{3}$ ≈1.7， $\sqrt{2}$ ≈1.4）．

查看试题解析
23. 如图，

(1)、在平面直角坐标系中作出△ABC以点O为位似中心，位似比为2的位似图形△A′B′C′；

(2)、点B′的坐标是（）；

(3)、△A′B′C′的面积是．

查看试题解析
24. 已知△ABC的两边AB、AC的长恰好是关于x的方程x²＋(2k＋3)x＋k²＋3k＋2＝0的两个实数根，第三边BC的长为5

(1)、求证：AB≠AC

(2)、如果△ABC是以BC为斜边的直角三角形，求k的值

(3)、填空：当k＝时，△ABC是等腰三角形，△ABC的周长为

查看试题解析
25. 某商店经销一种进价为每千克40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克．针对这种水产品的销售情况，请解答一下问题：

(1)、当销售单价定位每千克55元时，计算月销售量和月销售利润；

(2)、商店要使月销售利润为8000元，销售单价应定为多少？

查看试题解析
26. 我们定义：等腰三角形中底边与腰的比叫做底角的邻对(can)．如图，在△ABC中，AB＝AC，底角∠B的邻对记作canB，这时canB＝ $\frac{底边}{腰}$ ＝ $\frac{B C}{A B}$ .容易知道一个角的大小与这个角的邻对值是一一对应的，根据上述角的邻对的定义，解下列问题：

(1)、can30°＝；

(2)、如图②，已知在△ABC中，AB＝AC，canB＝ $\frac{8}{5}$ ，S_△_ABC＝24，求△ABC的周长．

查看试题解析

人员	店长	厨师甲	厨师乙	会计	服务员甲	服务员乙	勤杂工
人数	1	1	1	1	1	3	2
工资额	20000	7000	4000	2500	2200	1800	1200

	第一次	第二次	第三次	第四次
丁同学	80	80	90	90