河北省石家庄市桥东区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. sin30°的值为( )A、 B、 C、 D、2. 方程(x﹣2)2=0的根是( )A、2 B、﹣2 C、0 D、无解3. 函数y=- ,当x>0时的图象为( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,在△ABC中,DE∥BC , 若 ,则AE:AC等于( )
4. 如图,在△ABC中,DE∥BC , 若 ,则AE:AC等于( ) A、3:2 B、2:3 C、4:9 D、1:25. 如图,在⊙O中,点A是 的中点,∠AOB=40°,则∠ADC的度数是( )
A、3:2 B、2:3 C、4:9 D、1:25. 如图,在⊙O中,点A是 的中点,∠AOB=40°,则∠ADC的度数是( ) A、15° B、20° C、25° D、40°6. 在同一平面内,过已知A,B,C三个点可以作的圆的个数为( )A、0 B、1 C、2 D、0或17. 某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
A、15° B、20° C、25° D、40°6. 在同一平面内,过已知A,B,C三个点可以作的圆的个数为( )A、0 B、1 C、2 D、0或17. 某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
A、200(1+x)2=1000 B、200+200×2x=1000 C、200+200×3x=1000 D、200[1+(1+x)+(1+x)2]=10008. 如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到对应的△A′B′O.若点B的坐标是(-2,1),则点B′的坐标是( ) A、(-2,4) B、(-4,2) C、(2,-4) D、(4,-2)9. a,b是实数,点 、 在反比例函数 的图像上,则( )A、 B、 C、 D、10. 若⊙P的半径为5,圆心P的坐标为(-3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )A、在⊙P内 B、在⊙P上 C、在⊙P外 D、无法确定11. 若关于x的方程x2﹣ x+sina=0有两个相等的实数根,则锐角a为( )A、75° B、60° C、45° D、30°12. 已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm213. 如图,三角形纸片 的周长为 , ,⊙ 是 的内切圆,玲玲用剪刀在⊙ 的左侧沿着与⊙ 相切的任意一条直线 剪下一个 ,则 的周长是( )
A、(-2,4) B、(-4,2) C、(2,-4) D、(4,-2)9. a,b是实数,点 、 在反比例函数 的图像上,则( )A、 B、 C、 D、10. 若⊙P的半径为5,圆心P的坐标为(-3,4),则平面直角坐标系的原点O与⊙P的位置关系是( )A、在⊙P内 B、在⊙P上 C、在⊙P外 D、无法确定11. 若关于x的方程x2﹣ x+sina=0有两个相等的实数根,则锐角a为( )A、75° B、60° C、45° D、30°12. 已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的侧面积是( )A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm213. 如图,三角形纸片 的周长为 , ,⊙ 是 的内切圆,玲玲用剪刀在⊙ 的左侧沿着与⊙ 相切的任意一条直线 剪下一个 ,则 的周长是( )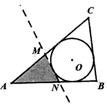 A、 B、 C、 D、根据 位置不同而变化14. 如图,点A在反比例函数y= (x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A、 B、 C、 D、根据 位置不同而变化14. 如图,点A在反比例函数y= (x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( ) A、3 B、2 C、 D、115. 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
A、3 B、2 C、 D、115. 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( ) A、5 B、8 C、 D、16. 如图,已知函数 与 的图象在第二象限交于点 ,点 在 的图象上,且点B在以O点为圆心,OA为半径的 上,则k的值为
A、5 B、8 C、 D、16. 如图,已知函数 与 的图象在第二象限交于点 ,点 在 的图象上,且点B在以O点为圆心,OA为半径的 上,则k的值为 A、 B、-1 C、 D、-2
A、 B、-1 C、 D、-2二、填空题
-
17. 如图,某游乐场一山顶滑梯的高为h , 滑梯的坡角为α,那么滑梯长l为 .
 18. 已知正六边形的边长为2,则它的内切圆的半径是 , 扇形AOB的面积 .
18. 已知正六边形的边长为2,则它的内切圆的半径是 , 扇形AOB的面积 . 19. 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F , 连接ED , 则DE的长度是 , B′D的最小值是 .
19. 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB′F , 连接ED , 则DE的长度是 , B′D的最小值是 .
三、解答题
-
20.(1)、解方程:x(x﹣1)=2;(2)、(1﹣sin45°)0﹣tan60°+ .21. 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y= 在第一象限内的图象分别交OA , AB于点C和点D , 连结OD , △BOD的面积是4.
 (1)、求反比例函数解析式;(2)、将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.22.
(1)、求反比例函数解析式;(2)、将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.22.已知,如图,== , 那么△ABD与△BCE相似吗?为什么?
 23. 如图,学校打算用16 m 的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如下图),面积是30 m2.求生物园的长和宽.
23. 如图,学校打算用16 m 的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如下图),面积是30 m2.求生物园的长和宽. 24. 为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据: ≈1.414, ≈1.732)
24. 为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据: ≈1.414, ≈1.732)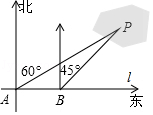 25. 如图, 是 的切线,切点为 , 是 的直径,连接 交 于 .过 点作 于点 ,交 于 ,连接 , .
25. 如图, 是 的切线,切点为 , 是 的直径,连接 交 于 .过 点作 于点 ,交 于 ,连接 , . (1)、求证: 是 的切线;(2)、求证: 为 的内心;(3)、若 , ,求 的长.26. 如图1,平行四边形ABCD中,AB⊥AC , AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A , E两点.
(1)、求证: 是 的切线;(2)、求证: 为 的内心;(3)、若 , ,求 的长.26. 如图1,平行四边形ABCD中,AB⊥AC , AB=6,AD=10,点P在边AD上运动,以P为圆心,PA为半径的⊙P与对角线AC交于A , E两点. (1)、线段AC的长度是 .(2)、如图2,当⊙P与边CD相切于点F时,求AP的长;(3)、不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .
(1)、线段AC的长度是 .(2)、如图2,当⊙P与边CD相切于点F时,求AP的长;(3)、不难发现,当⊙P与边CD相切时,⊙P与平行四边形ABCD的边有三个公共点,随着AP的变化,⊙P与平行四边形ABCD的边的公共点的个数也在变化,若公共点的个数为4,直接写出相对应的AP的值的取值范围 .