河北省秦皇岛市抚宁区留守营学区2019-2020学年九年级上学期数学期中试卷
试卷更新日期：2020-09-25 类型：期中考试
一、单选题
-
1. 某校组织了“讲文明、守秩序、迎南博”知识竞赛活动，从中抽取了7名同学的参赛成绩如下（单位：分）：80，90，70，100，60，80，80．则这组数据的中位数和众数分别是（ ）A、90，80 B、70，80 C、80，80 D、100，802. 某中学规定学生的学期体育成绩满分为100分，其中课外体育占20%，期中考试成绩占30%，期末考试成绩占50%.小彤的这三项成绩（百分制）分别为95分，90分，88分，则小彤这学期的体育成绩为（ ）A、89分 B、90分 C、92分 D、93分3. 一元二次方程 的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根4. 用配方法解一元二次方程
时，原方程可变形为（ ） A、 B、 C、 D、5. 下列命题正确的是（ ）A、所有的直角三角形都相似 B、所有的等腰三角形都相似 C、两个半径不等的圆相似 D、有一个角是30°的等腰三角形都相似6. 为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高（单位：cm）的平均数与方差为： = =13， = =15：s甲2=s丁2=3.6，s乙2=s丙2=6.3．则麦苗又高又整齐的是（ ）
A、甲 B、乙 C、丙 D、丁7. 如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，则图中相似三角形共有（ ）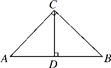
A、1对 B、2对 C、3对 D、4对8.如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（ ）
A、AB=24m B、MN∥AB C、△CMN∽△CAB D、CM：MA=1：29. 上海世博会的某纪念品原价168元，连续两次降价a%后售价为128元，下面所列方程中正确的是（ ）A、168(1＋a%)2＝128 B、168(1－a%)2＝128 C、168(1－2a%)＝128 D、168(1－a2%)＝12810. 如果等腰三角形的两边长分别是方程x2－10x＋21＝0的两根，那么它的周长为（ ）A、17 B、15 C、13 D、13或1711. 如果一组数据a1 ， a 2 ， a3 ， ⋯ ，an ， 方差是2，那么一组新数据2a1 ， 2a2 ， ⋯ ，2an的方差是（ ）A、2 B、4 C、8 D、1612. 某校有两块相似的多边形草坪，其面积比为9∶4，其中一块草坪的周长是36米，则另一块草坪的周长是（ ）A、24米 B、54米 C、24米或54米 D、36米或54米13. 在平行四边形 中， 是 上一点，连接 并延长交 的延长线于点 ，则下列结论错误的是（ ）
A、 B、 C、 D、14. 南京青奥会的3人篮球赛，要求参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排5天，每天安排3场比赛．这次青奥会共有x个队参赛，则x满足的关系式为（ ）A、 x(x＋1)＝15 B、 x(x－1)＝15 C、x(x＋1)＝15 D、x(x－1)＝15二、填空题
-
15. 把一元二次方程3x2+1=7x化为一般形式是 ．16. 若x=1是一元二次方程x2+2x+a=0的一个根，那么a= .
17. 大唐芙蓉园位于古都西安大雁塔东侧，是中国第一个全方位展示盛唐风貌的大型皇家园林式文化主题公园．该园占地面积约为800000m2 ， 小明按比例尺1∶2000缩小后画出该园示意图，其面积大约为m2 ．18. 学校篮球队五名队员的年龄分别为 ，其方差为 ，则三年后这五名队员年龄的方差为 ．19. 甲、乙两地9月上旬的日平均气温如图所示，则甲、乙两地这10天日平均气温方差大小关系为s甲2s乙2(填“＞”或“＜”)．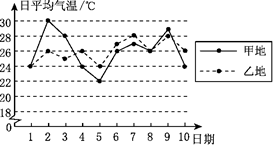
20. 已知三角形ABC的三边长分别为5、12、13，与其相似的 的最大边长为26，则 的面积为 ．三、解答题
-
21. 解方程(1)、 （配方法）(2)、3x（x﹣2）=2（2﹣x）(方法自选)22. 在13×13的网格图中，已知△ABC和点M(1，2)．
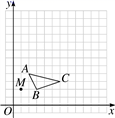(1)、以点M为位似中心，画出△ABC的位似图形△A′B′C′，其中△A′B′C′与△ABC的位似比为2；(2)、写出△A′B′C′的各顶点坐标．23. “最美女教师”张丽莉，为抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款，我市某中学九年级一班全体同学参加了捐款活动，该班同学捐款情况的部分统计图如图所示：
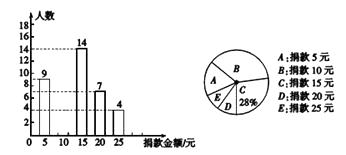(1)、求该班的总人数；(2)、将条形图补充完整，并写出捐款总额的众数；
(3)、该班平均每人捐款多少元？
24.如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．
(1)、求证：△ADE∽△ABC；(2)、若AD=3，AB=5，求 的值．25. 某商店如果将进货价为8元的商品按每件10元售出，每天可销售200件．现在采取提高售价，减少售货量的方法增加利润，已知这种商品每涨价0.5元，其销量减少10件．(1)、若涨价x元，则每天的销量为件（用含x的代数式表示）；(2)、要使每天获得700元的利润，请你帮忙确定售价．26. 如图所示，△ABC中，∠C=90°，BC=8cm，AC：AB=3：5，点P从点B出发沿BC向点C以2cm/s的速度移动，点Q从点C出发沿CA向点A以1cm/s的速度移动，如果P、Q分别从B、C同时出发：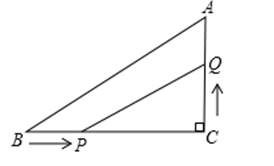
(1)、经过多少秒后，△CPQ的面积为8cm？(2)、经过多少秒时，以C、P、Q为顶点的三角形恰与△ABC相似？