河北省沧州泊头市2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-25 类型：期中考试

进入出卷网下载

一、单选题

1. $\frac{1}{3} \cos 30 °$ 的值为（）

A、 $\frac{\sqrt{3}}{6}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{6}$ D、 $\frac{\sqrt{2}}{6}$

查看试题解析
2. 若 $\frac{a}{b} = \frac{11}{5}$ ，则 $\frac{a - b}{a + b}$ 的值是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{8}$ C、 $\frac{3}{5}$ D、 $\frac{11}{5}$

查看试题解析
3. 一元二次方程3x²﹣x﹣2＝0的二次项系数是3，它的一次项系数是（）

A、﹣1 B、﹣2 C、1 D、0

查看试题解析
4. 甲、乙、丙三个旅游团的游客人数都相等，且每个团游客的平均年龄都是35岁，这三个团游客年龄的方差分别是S_甲²=1.4，S_乙²=18.8，S_丙²=25，导游小方最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选( )

A、甲队 B、乙队 C、丙队 D、哪一个都可以

查看试题解析
5. 在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”，“兵”所在位置的格点构成的三角形相似（）

A、①处 B、②处 C、③处 D、④处

查看试题解析
6. 如图，水库大坝的横断面为梯形，坝顶宽6米，坝高8米，斜坡AB的坡角为45°，斜坡CD的坡度为1：3，则坝底宽BC为（）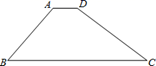

A、36米 B、72米 C、78米 D、38米

查看试题解析
7. 若关于x的方程（m﹣1）x²+2x+1＝0有实数解，则m的取值范围是（）

A、m≤2 B、m≤ $\frac{1}{2}$ C、m≤2且m≠1 D、m＜2

查看试题解析
8. 某水果种植基地 $2016$ 年产量为 $80$ 吨，截止到 $2018$ 年底，三年总产量达到 $300$ 吨，求三年中该基地水果产量的年平均增长率.设水果产量的年平均年增长率为 $x$ ，则可列方程为（）

A、 $80 {(1 + x)}^{2} = 300$ B、 $80 (1 + 3 x) = 300$ C、 $80 + 80 (1 + x) + 80 {(1 + x)}^{2} = 300$ D、 $80 {(1 + x)}^{3} = 300$

查看试题解析
9. 古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 $\frac{\sqrt{5} - 1}{2}$ ( $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ，称为黄金比例)，如图，著名的“断臂维纳斯”便是如此，此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是 $\frac{\sqrt{5} - 1}{2}$ ，若某人的身材满足上述两个黄金比例，且头顶至咽喉的长度为 $26 c m$ ，则其升高可能是（）

A、 $165 c m$ B、 $178 c m$ C、 $185 c m$ D、 $190 c m$

查看试题解析
10. 如图，在△ABC中，AB＝7cm，AC＝4cm，点D从B点以每秒2cm的速度向点A移动，点E从A点以每秒1cm的速度向点C移动，若D、E同时出发，同时停止．则经过多少时间△ADE与△ABC相似．（）

A、 $\frac{28}{15}$ （s） B、 $\frac{7}{3}$ （s） C、 $\frac{28}{15}$ （s）或 $\frac{49}{18}$ （s） D、 $\frac{7}{3}$ （s）或 $\frac{49}{18}$ （s）

查看试题解析

二、填空题

11. 在比例尺为1:8000 000地图上测得甲、乙两地间的图上距离为4厘米，那么甲、乙两地间的实际距离为千米

查看试题解析
12. 若△ABC～△DEF，面积比为9：4，则△ABC与DEF对应中线的比为.

查看试题解析
13. 已知关于x的方程（a﹣3）x^|a^﹣^1|+x﹣1＝0是一元二次方程，则a=.

查看试题解析
14. 在△ABC中， $\sqrt{\sin A - 0.5}$ +|tanB﹣ $\sqrt{3}$ |＝0，则△ABC是三角形．

查看试题解析
15. 如果一组数据7、6、9、6、x、7的众数是6，那么这组数据的中位数是.

查看试题解析
16. 烹饪大赛的菜品的评价按味道、外形、色泽三个方面进行评价（评价的满分均为100分），三个方面的重要性之比依次为7：2：1．某位厨师的菜所得的分数依次为92分、88分、80分，那么这位厨师的最后得分是．

查看试题解析
17. a是方程x²+x﹣1＝0的一个根，则代数式a³+2a²+2018＝．

查看试题解析
18. 如图，在平行四边形ABCD中，E在DC上，若DE：EC=2：3，则AF：AC=.

查看试题解析
19. 如图，已知Rt△AC₁C中，∠AC₁C＝90°，∠A＝30°，CC₁＝1，作C₁C₂⊥AC于点C₂ ， C₂C₃⊥AC₁于点C₃ ， C₃C₄⊥AC于点C₄……C_n_﹣₁C_n⊥…于点C_n ，分別记线段CC₁ ， C₁C₂ ， C₂C₃…C_n_﹣₁C_n的长为a₁ ， a₂ ， a₃…a_n ，计算并观察其中的规律得a_n＝.

查看试题解析

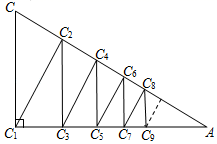
三、解答题

20. “今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形城池ABCD ，东边城墙AB长9里，南边城墙AD长7里，东门点E ，南门点F分别是AB、AD的中点，EG⊥AB ， FH⊥AD ， EG＝15里，HG经过点A ，问FH多少里？

查看试题解析
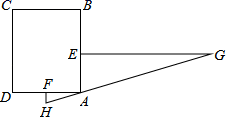21. 如图所示，在边长为1的正方形网格中，建立如下平面直角坐标系中其中△ABO的顶点A（3，4）、B（8，1）、O（0，0）

(1)、以O为位似中心，在第一象限内作出△ABO的位似图形△A₁B₁O，其相似比为 $\frac{1}{2}$ ．

(2)、将△ABO绕点O逆时针旋转90°得到△A₂B₂O

查看试题解析
22. 用适当的方法解下列方程．

(1)、x²﹣8x﹣2＝0

(2)、x（x﹣3）＝﹣x+3

查看试题解析
23. 如图是某市连续5天的天气情况.

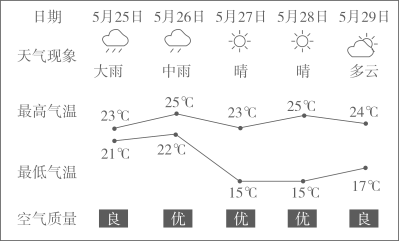(1)、利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大；

(2)、根据如图提供的信息，请再写出两个不同类型的结论.

查看试题解析
24. 如图，游客在点A处坐缆车出发，沿A﹣B﹣D的路线可至山顶D处.已知AB＝BD＝800米，∠α＝75°，∠β＝45°，求山高DE（结果精确到1米）.（参考数据：sin75°＝0.966，cos75°＝0.259，tan75°＝3.732， $\sqrt{2}$ ＝1.414）

查看试题解析
25. 某农场要建一个饲养场（矩形ABCD）两面靠现有墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）。建成后木栏总长45米。设饲养场（矩形ABCD）的一边AB长为x米.

(1)、饲养场另一边BC=米（用含x的代数式表示）.

(2)、若饲养场的面积为180平方米，求x的值.

查看试题解析
26. 小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．

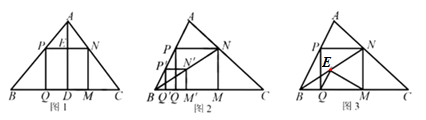(1)、温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB， AC上，若BC=6，AD=4，求正方形PQMN的边长．

(2)、操作：能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P′，画正方形P′Q′M′N′，使Q′，M′在BC边上，N′在△ABC内，连结B N′并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN．小波把线段BN称为“波利亚线”．
推理：证明图2中的四边形PQMN是正方形．

(3)、拓展：在(2)的条件下，于波利业线B N上截取NE=NM，连结EQ，EM(如图3)．当tan∠NBM= $\frac{3}{4}$ 时，猜想∠QEM的度数，并尝试证明．
请帮助小波解决“温故”、“推理”、“拓展”中的问题．

查看试题解析