河北省保定市蠡县2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 下列函数是二次函数的是( )A、y=2x+2 B、y=﹣2x C、y=x2+2 D、y=x﹣22. 一元二次方程x2-2(3x-2)+(x+1)=0的一般形式是( )A、x2-5x+5=0 B、x2+5x-5=0 C、x2+5x+5=0 D、x2+5=03. 下列图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 4. 如右图,⊿ABC内接于⊙O,若∠OAB=28°则∠C的大小为( )
4. 如右图,⊿ABC内接于⊙O,若∠OAB=28°则∠C的大小为( )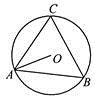 A、62° B、56° C、60° D、28°5. 用配方法解方程x2﹣2x﹣5=0时,原方程应变形为( )A、(x+1)2=6 B、(x+2)2=9 C、(x﹣1)2=6 D、(x﹣2)2=96. 已知 是关于x的二次函数,且有最大值,则k=( )A、﹣2 B、2 C、1 D、﹣17. 下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③ 相等的圆心角所对的弧相等.其中真命题的是( )
A、62° B、56° C、60° D、28°5. 用配方法解方程x2﹣2x﹣5=0时,原方程应变形为( )A、(x+1)2=6 B、(x+2)2=9 C、(x﹣1)2=6 D、(x﹣2)2=96. 已知 是关于x的二次函数,且有最大值,则k=( )A、﹣2 B、2 C、1 D、﹣17. 下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③ 相等的圆心角所对的弧相等.其中真命题的是( )
A、①② B、②③ C、①③ D、①②③8. 如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )A、 B、
B、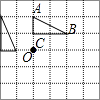 C、
C、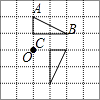 D、
D、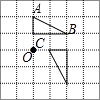 9. 两年内某校办工厂的利润由5万元增长到9万元,设每年利润的平均增长率为x , 可以列方程得:( )A、5(1+x)=9 B、5(1+x)2=9 C、5(1+x)+5(1+x)2=9 D、5+5(1+x)+5(1+x)2=910. 抛物线y=(x+3)2﹣4可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A、先向左平移3个单位,再向上平移4个单位 B、先向左平移3个单位,再向下平移4个单位 C、先向右平移3个单位,再向下平移4个单位 D、先向右平移3个单位,再向上平移4个单位11. 如果|3﹣a|+(b+5)2=0,那么点A(a,b)关于原点对称的点A′的坐标为( )A、(3,5) B、(3,﹣5) C、(﹣3,5) D、(5,﹣3)12. 下列方程中没有实数根的是( )A、x2﹣x﹣1=0 B、x2+2x+1=0 C、2019x2+11x﹣20=0 D、x2﹣2x+7=013.
9. 两年内某校办工厂的利润由5万元增长到9万元,设每年利润的平均增长率为x , 可以列方程得:( )A、5(1+x)=9 B、5(1+x)2=9 C、5(1+x)+5(1+x)2=9 D、5+5(1+x)+5(1+x)2=910. 抛物线y=(x+3)2﹣4可以由抛物线y=x2平移得到,则下列平移过程正确的是( )A、先向左平移3个单位,再向上平移4个单位 B、先向左平移3个单位,再向下平移4个单位 C、先向右平移3个单位,再向下平移4个单位 D、先向右平移3个单位,再向上平移4个单位11. 如果|3﹣a|+(b+5)2=0,那么点A(a,b)关于原点对称的点A′的坐标为( )A、(3,5) B、(3,﹣5) C、(﹣3,5) D、(5,﹣3)12. 下列方程中没有实数根的是( )A、x2﹣x﹣1=0 B、x2+2x+1=0 C、2019x2+11x﹣20=0 D、x2﹣2x+7=013.数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
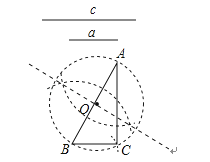 A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径14. 我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )A、x1=1,x2=3 B、x1=1,x2=﹣3 C、x1=﹣1,x2=3 D、x1=﹣1,x2=﹣315. 在同一坐标系内,一次函数 y=ax+b 与二次函数 y=ax2+8x+b 的图象可能是( )A、
A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径14. 我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )A、x1=1,x2=3 B、x1=1,x2=﹣3 C、x1=﹣1,x2=3 D、x1=﹣1,x2=﹣315. 在同一坐标系内,一次函数 y=ax+b 与二次函数 y=ax2+8x+b 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 16. 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为( )
16. 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为( ) A、 B、1 C、 或1 D、 或1或
A、 B、1 C、 或1 D、 或1或二、填空题
-
17. 已知⊙O中,弦AB=8cm,圆心到AB的距离为3cm,则此圆的半径为
18. 如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是 . 19. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
19. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:x
…
﹣1
0
1
2
3
…
y
…
m
5
2
1
2
…
则m的值是 , 当y<5时,x的取值范围是 .
三、解答题
-
20. 解方程:(1)、x2﹣2x=4(2)、(x﹣3)(x﹣1)=321. 已知关于x的一元二次方程x2+2(k﹣1)x+k2﹣1=0有两个不相等的实数根.(1)、求实数k的取值范围;(2)、0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.22. 如图所示,二次函数 的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
 (1)、求m的值;(2)、求点B的坐标;(3)、该二次函数图象上有一点D(x,y)(其中 , ),使 ,求点D的坐标.23. 如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6,求阴影部分面积.
(1)、求m的值;(2)、求点B的坐标;(3)、该二次函数图象上有一点D(x,y)(其中 , ),使 ,求点D的坐标.23. 如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6,求阴影部分面积. 24. 根据要求,解答下列问题.(1)、根据要求,解答下列问题.
24. 根据要求,解答下列问题.(1)、根据要求,解答下列问题.①方程x2-2x+1=0的解为;
②方程x2-3x+2=0的解为;
③方程x2-4x+3=0的解为;
…… ……
(2)、根据以上方程特征及其解的特征,请猜想:①方程x2-9x+8=0的解为;
②关于x的方程的解为x1=1,x2=n.
(3)、请用配方法解方程x2-9x+8=0,以验证猜想结论的符合题意性.25. 如图,已知△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△ABC的位置,连接C'B.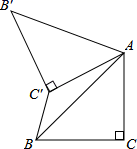 (1)、求∠ABC'的度数;(2)、求C'B的长.26. 某货车销售公司,分别试销售两种型号货车各一个月,并从中选择一种长期销售,设每月销售量为x辆若销售甲型货车,每月销售的利润为y1(万元),已知每辆甲型货车的利润为(m+6)万元,(m是常数,9≤m≤11),每月还需支出其他费用8万元,受条件限制每月最多能销售甲型货车25辆;若销售乙型货车,每月的利润y2(万元)与x的函数关系式为y2=ax2+bx-25,且当x=10时,y2=20,当x=20时,y2=55,受条件限制每月最多能销售乙型货车40辆.(1)、分别求出y1、y2与x的函数关系式,并确定x的取值范围;(2)、分别求出销售这两种货车的最大月利润;(最大利润能求值的求值,不能求值的用式子表示)(3)、为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
(1)、求∠ABC'的度数;(2)、求C'B的长.26. 某货车销售公司,分别试销售两种型号货车各一个月,并从中选择一种长期销售,设每月销售量为x辆若销售甲型货车,每月销售的利润为y1(万元),已知每辆甲型货车的利润为(m+6)万元,(m是常数,9≤m≤11),每月还需支出其他费用8万元,受条件限制每月最多能销售甲型货车25辆;若销售乙型货车,每月的利润y2(万元)与x的函数关系式为y2=ax2+bx-25,且当x=10时,y2=20,当x=20时,y2=55,受条件限制每月最多能销售乙型货车40辆.(1)、分别求出y1、y2与x的函数关系式,并确定x的取值范围;(2)、分别求出销售这两种货车的最大月利润;(最大利润能求值的求值,不能求值的用式子表示)(3)、为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.