山西省运城市垣曲县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 2的平方根为( )A、4 B、±4 C、 D、±2. 下列计算正确的是( )A、 B、 C、 D、3. 若点A(a,b)在第三象限,则点B(a,-b)在第( )象限A、一 B、二 C、三 D、四4. 一个正比例函数的图象经过(2,-1),则它的表达式为 )A、y=-2x B、y=2x C、 D、5. 一次函数 , ,且y随x的增大而减小,则其图象可能是( )A、
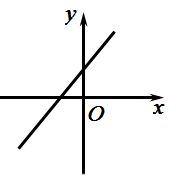 B、
B、 C、
C、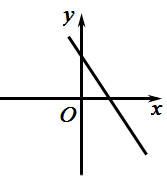 D、
D、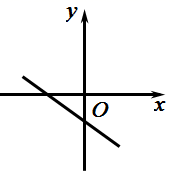 6. 一次函数 的图象如图所示,则关于x的方程 的解为( )
6. 一次函数 的图象如图所示,则关于x的方程 的解为( )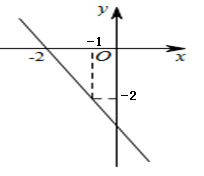 A、 B、 C、 D、7. 如图,在平面直角坐标系中A(-4,0),B(0,3),P是线段AB上的一个动点,则OP的最小值是( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中A(-4,0),B(0,3),P是线段AB上的一个动点,则OP的最小值是( )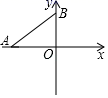 A、3 B、4 C、 D、8. 小明同学测量了等腰三角形的腰、底边和底边上的高的长,但他把这三个数据与其他数据弄混了,请你帮他找出正确的那组是( )A、13,12,8 B、4,8,5 C、13,5,12 D、12,8,109. 如图,OA和BA分别表示甲乙两名学生练习跑步的一次函数的图象,图中S和t分别表示路程(米)和时间(秒),根据图象判定跑210米时,快者比慢者少用( )秒.
A、3 B、4 C、 D、8. 小明同学测量了等腰三角形的腰、底边和底边上的高的长,但他把这三个数据与其他数据弄混了,请你帮他找出正确的那组是( )A、13,12,8 B、4,8,5 C、13,5,12 D、12,8,109. 如图,OA和BA分别表示甲乙两名学生练习跑步的一次函数的图象,图中S和t分别表示路程(米)和时间(秒),根据图象判定跑210米时,快者比慢者少用( )秒.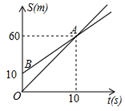 A、4秒 B、3.5秒 C、5秒 D、3秒10. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( )
A、4秒 B、3.5秒 C、5秒 D、3秒10. 勾股定理在平面几何中有着不可替代的重要地位,在我国古算书(周髀算经》中就有“若勾三,股四,则弦五”的记载,如图1是由边长均为1的小正方形和Rt△ABC构成的,可以用其面积关系验证勾股定理,将图1按图2所示“嵌入”长方形LMJK,则该长方形的面积为( ) A、120 B、110 C、100 D、90
A、120 B、110 C、100 D、90二、填空题
-
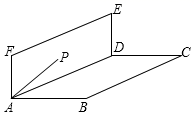
11. 写出一个比 大的负无理数.12. 若a,b为两个连续的正整数,且 ,则 .13. 若点A(1, )和点B(2, )都在一次函数 的图象上,则 .(填“>”、“<”或“=”)14. 若直线 和直线 的交点在y轴上,则m=.15. 已知点P在y轴负半轴上,且到x轴的距离是2,那么点P的坐标是.点M与点P之间距离是3,且PM与x轴平行,则点M的坐标是.16. 如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上,若PA=5,AB=8,点P到AD的距离是3,有一只蚂蚁要从点P爬到点B,它的最短行程是.
三、解答题
-
17. 计算(1)、(2)、(3)、(4)、18. 已知a,b为实数,且满足(1)、求a,b的值:(2)、若a,b为△ABC的两边,第三边c为 ,求△ABC的面积.19.(1)、作出函数 的图象,并利用图象回答问题:
 (2)、写出图象与x轴的交点A的坐标 , 与y轴的交点B的坐标.(3)、当 时,y的取值范围是.(4)、有一点C的坐标是(3,4),顺次连接点A、B、C得到△ABC,三角形ABC的面积为.(5)、点C关于x轴对称的点D的坐标(6)、连接B,D两点,求直线BD的函数关系式.20. 大家知道 是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为 ,所以可用、 来表示 的小数部分.请解答下列问题:(1)、 的整数部分是 , 小数部分是.(2)、如果 的整数部分为a,小数部分为b,求 的值.(3)、已知 ,其中x是整数,且 .则求 的平方根的值.21. 阅读下面的情景对话,然后解答问题:
(2)、写出图象与x轴的交点A的坐标 , 与y轴的交点B的坐标.(3)、当 时,y的取值范围是.(4)、有一点C的坐标是(3,4),顺次连接点A、B、C得到△ABC,三角形ABC的面积为.(5)、点C关于x轴对称的点D的坐标(6)、连接B,D两点,求直线BD的函数关系式.20. 大家知道 是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为 ,所以可用、 来表示 的小数部分.请解答下列问题:(1)、 的整数部分是 , 小数部分是.(2)、如果 的整数部分为a,小数部分为b,求 的值.(3)、已知 ,其中x是整数,且 .则求 的平方根的值.21. 阅读下面的情景对话,然后解答问题:老师:我们定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形中是否存在奇异三角形呢?
(1)、:根据“奇异三角形”的定义,请你判断小华提出的猜想:“等边三角形一定是奇异三角形”是否符合题意?.(填“是”或“否”)(2)、:已知RtΔABC中,两边长分别是 ,10,若这个三角形是奇异三角形,则第三边是.(3)、:如图,以AB为斜边分别在AB的两侧作直角三角形,且AD=BD,若四边形ADBC内存在点E,使得AE=AD,CB=CE.试说明:△ACE是奇异三角形.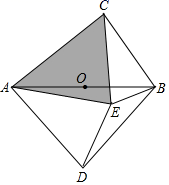 22. 运城的桃子今年获得了大丰收,现A,B两个水果合作社要向甲,乙两个市场运送桃子,已知A可调出110吨,B可调出90吨,甲地需要80吨,乙地需要120吨,两地到甲乙市场的路程和费用如图:
22. 运城的桃子今年获得了大丰收,现A,B两个水果合作社要向甲,乙两个市场运送桃子,已知A可调出110吨,B可调出90吨,甲地需要80吨,乙地需要120吨,两地到甲乙市场的路程和费用如图:路程(km)
A地
B地
甲农贸市场
15
20
乙农贸市场
22
25
(1)、设A地运往甲市场的桃子x吨(0≤x≤80),则A地运往乙市场的桃子有吨,B地运往甲市场的桃子有吨,B地运往乙市场的桃子有吨.(2)、若每吨桃子每千米需要运费12元,求总运费y(元)关于x(吨)的函数关系式;(3)、当A地给甲农贸市场运多少吨桃子时,总运费最省?最省的总运费是多少?23. 如图,平面直角坐标系中,一次函数 的图像与x轴交于点A,与y轴交于点B,点C是直线AB上一点,它的坐标为(m,2),经过点C作直线CD∥轴交y轴于点D.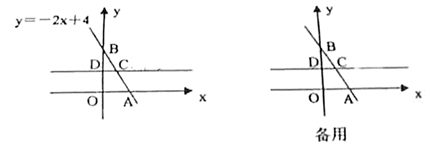 (1)、求点C的坐标及线段AB的长;(2)、已知点P是直线CD上一点.
(1)、求点C的坐标及线段AB的长;(2)、已知点P是直线CD上一点.①若△POC的面积是4,求点P的坐标;
②若△POC是直角三角形,请直接写出所有满足条件的点P的坐标.