山西省忻州市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 下图是几种汽车的标志,其中属于轴对称图形的有( )
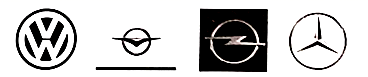 A、1个 B、2个 C、3个 D、4个2. 以下列各组线段为边,能组成三角形的是( )A、2,3,5 B、2,3,6 C、8,6,4 D、6,7,143. 若 ,且 , , ,则 的长为( )A、6 B、8 C、9 D、104. 如图,点D,E分别在线段 , 上, 与 相交于点P,已知 .现添加以下哪个条件仍不能判定 ( )
A、1个 B、2个 C、3个 D、4个2. 以下列各组线段为边,能组成三角形的是( )A、2,3,5 B、2,3,6 C、8,6,4 D、6,7,143. 若 ,且 , , ,则 的长为( )A、6 B、8 C、9 D、104. 如图,点D,E分别在线段 , 上, 与 相交于点P,已知 .现添加以下哪个条件仍不能判定 ( ) A、 B、 C、 D、5. 如图,点A在直线 上, 与 关于直线l对称,连接 分别交 , 于点D, ,连接 .下列结论不一定正确的是( )
A、 B、 C、 D、5. 如图,点A在直线 上, 与 关于直线l对称,连接 分别交 , 于点D, ,连接 .下列结论不一定正确的是( )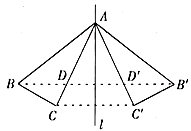 A、 B、 C、 D、6. 已知一个多边形的每个内角都为 ,则从该多边形的一个顶点出发可引对角线( )A、8条 B、7条 C、6条 D、5条7. 复习课上,老师给出一个问题:“已知等腰三角形的一边等于5,另一边等于7,求该等腰三角形的周长.”小红代表小组发言:“等腰三角形的边分为腰和底边,所以第一种情况:5是腰长,7是底边长;第二种情况:5是底边长,7是腰长,所以周长为17或19.”小红的上述方法体现的数学思想是( )A、分类讨论 B、数形结合 C、转化思想 D、类比思想8. 如图,在 中, 垂直平分 ,交 于点E,连接 ,若 , ,则 的周长为( )
A、 B、 C、 D、6. 已知一个多边形的每个内角都为 ,则从该多边形的一个顶点出发可引对角线( )A、8条 B、7条 C、6条 D、5条7. 复习课上,老师给出一个问题:“已知等腰三角形的一边等于5,另一边等于7,求该等腰三角形的周长.”小红代表小组发言:“等腰三角形的边分为腰和底边,所以第一种情况:5是腰长,7是底边长;第二种情况:5是底边长,7是腰长,所以周长为17或19.”小红的上述方法体现的数学思想是( )A、分类讨论 B、数形结合 C、转化思想 D、类比思想8. 如图,在 中, 垂直平分 ,交 于点E,连接 ,若 , ,则 的周长为( )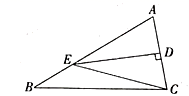 A、 B、 C、 D、9. 一个等腰三角形一腰上的高与另一腰的夹角为 ,则该等腰三角形顶角的度数为( )A、 B、 或 C、 或 D、 或10. 如图, ,点 在 边上,线段 与 交于点D.若 , ,则 的度数( )
A、 B、 C、 D、9. 一个等腰三角形一腰上的高与另一腰的夹角为 ,则该等腰三角形顶角的度数为( )A、 B、 或 C、 或 D、 或10. 如图, ,点 在 边上,线段 与 交于点D.若 , ,则 的度数( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 埃及金字塔、屋顶、埃菲尔铁塔等建筑中都能找到三角形的形状,这是由于三角形具有.12. 如图,在 中, , 的平分线 , 相交于点F, ,则 的度数为.
 13. 如图,在 中, , 于D,点E、F是 的三等分点,若 的面积为 ,则图中阴影部分的面积 .
13. 如图,在 中, , 于D,点E、F是 的三等分点,若 的面积为 ,则图中阴影部分的面积 . 14. 如图,在平面直角坐标系中, , ,P是x轴上一个动点,当 的值最小时,点P的坐标为.
14. 如图,在平面直角坐标系中, , ,P是x轴上一个动点,当 的值最小时,点P的坐标为. 15. 如图: , , ,若 ,则 等于.
15. 如图: , , ,若 ,则 等于.
三、解答题
-
16. 如图, 的顶点都在正方形网格的格点上,点
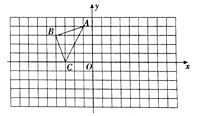
⑴作出 关于y轴的对称图形 ,写出点A的对应点 的坐标
⑵作出 关于x轴的对称图形 ,写出点A的对应点 的坐标
⑶观察图形,说一说点 和点 的坐标有什么特点.
17. 如图,AC=DF,AD=BE,BC=EF.求证: AC∥DF. 18. 要将图中的 平分,小强设计如下方案:
18. 要将图中的 平分,小强设计如下方案:在射线 , 上分别取 ,过点A作 于A,交 于D;过点 作 于点B,交 于E, , 交于点C,过点O、点C作射线 ,射线 即为 的平分线.请说明这样做的理由.
 19. 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
19. 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点. (1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法);
(1)、实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法);①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
(2)、猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.20. 如图,锐角 中,高 和 交于点H,且 ,求 的度数. 21. 如图,在平面直角坐标系中, 的顶点A、C分别在y轴、x轴上,且 , , , ,点B在第一象限时,求点B的坐标.
21. 如图,在平面直角坐标系中, 的顶点A、C分别在y轴、x轴上,且 , , , ,点B在第一象限时,求点B的坐标. 22. 阅读下列材料,并完成相应的任务.
22. 阅读下列材料,并完成相应的任务.基本性质:三角形中线等分三角形的面积.
如图, 是 的边 上的中线,

则
理由:过点A作 于点H
∵ 是 的边 上的中线.
∴ 又∵ ,
∴
∴三角形中线等分三角形的面积.
任务:
(1)、如图,延长 的边 到点D,使 ,连接 ,则 和 的数量关系为. (2)、如图,点D是 的边 上任意一点,点 分别是线段 , 的中点,且 的面积为 ,请同学们借助上述结论求 的面积.
(2)、如图,点D是 的边 上任意一点,点 分别是线段 , 的中点,且 的面积为 ,请同学们借助上述结论求 的面积. 23. 综合与实践
23. 综合与实践已知 是等腰直角三角形, , ,D为 的中点.
(1)、如图:过D作 ,分别交 、 于M、N.求证: . (2)、如图,若 ,分别与 、 的延长线交于点M、N,此时(1)中的结论还成立吗?若成立,请说明理由,若不成立,请举例说明.
(2)、如图,若 ,分别与 、 的延长线交于点M、N,此时(1)中的结论还成立吗?若成立,请说明理由,若不成立,请举例说明.