山西省吕梁市孝义市2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-09-25 类型：期中考试
一、单选题
-
1. 下列各组图案中，不是全等形的是（ ）A、
B、
C、
D、
2. 三角形的重心是（ ）A、三角形三条边上中线的交点 B、三角形三条边上高线的交点 C、三角形三条边垂直平分线的交点 D、三角形三条内角平行线的交点3. 凸多边形中，四边形有2条对角线，五边形有5条对角线，十五边形对角线的条数是（ ）A、35条 B、77条 C、80条 D、90条4. 一个正多边形的一个外角是72°，则这个多边形是（ ）A、三角形 B、五边形 C、六边形 D、七边形5. 如图，点C，F在AD上，AB=DE，AF=DC，要使ΔABC≌ΔDEF，可以添加的一个条件是（ ）
A、AB∥DE B、EF∥BC C、∠B=∠E D、∠ACB=∠DFE6. 下列银行标志中，是轴对称图形的是（ ）A、
B、
C、
D、
7. 已知点A(m+1，-2m+3)关于x轴的对称点在第四象限，则m的取值范围是（ ）A、 B、 C、 D、8. 如图，在△ABC中，AB=AC，点EF是中线AD上的两点，则图中全等三角形有几对（ ）
A、4对 B、5对 C、6对 D、7对9. 如图，ΔABC中，三条中线AD，BE，CF相交于点O，若ΔABC的面积是10，则△OCD的面积是（ ）
A、2 B、1.5 C、 D、510. 如图，将长方形纸片ABCD沿BE折叠，使点C落在AD边的C′处，若△ABC′的周长是12，ΔDEC′的周长是4，则BC′+EC′+DE的长为（ ）
A、4 B、6 C、8 D、12二、填空题
-
11. 如图，若已知AC=DB．∠ACB=∠DBC，BC=BC，则可推出ΔABC≌ΔDCB，依据是.
12. 我们得到“三角形两边的和大于第三边”的依据是.13. 一个多边形纸片剪掉一个角后，形成的多边形的内角和是720°，则原多边形的边数是.14. 如图，RtΔABC中，∠ACB=90°，AB：AC：BC=5：4：3，CD是AB边上的中线，DE⊥BC，DF⊥AC．则DE：DF=.
15. 如图，Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AB，AC于点E，D，再分别以D，E为圆心，大于 DE的长为半径画弧，两弧交于点F，作射线AF交BC于点C，若AB=5cm，CG=2cm，则ΔABG的面积是.
16. 如图，∠AOB=40°，点P在∠AOB的内部，点C，D分别是点P关于直线OA，OB的对称点，连接CD分别交OA，OB于点E、F.则∠EPF=.
三、解答题
-
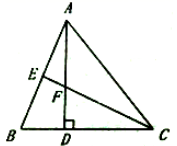
17. 如图，已知△ABC中，AD是BC边上的高，CE平分∠ACB，AD与CE相交于点F.∠B=65°，∠AFC=120°，求∠BAD和∠ACB的度数.
18. 已知：如图，点A，B，C，D在同一直线上，AE∥DF，BF∥EC，AB=CD．求证：AE=DF.
19. 作图题.如图，已知△ABC，求作Δ ，使 =AB，∠ =∠B， =BC．(尺规作图，不写作法，保留作图痕迹，作在右侧方框内)
20. 如图，△ABC中，已知点A(-1，4)，B(-2，2)，C(1，1).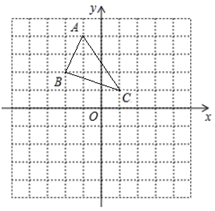
(1)、作ΔABC关于x轴对称的△A1B1C1 ， 并写出点A1 ， B1 ， C1的坐标，(2)、作△ABC关于y轴对称的△A2B2C2 ， 并写出点A2 ， B2 ， C2的坐标，(3)、观察点A1 ， B1 ， C1和A2 ， B2 ， C2的坐标，请用文字语言归纳点A1和A2 ， B1和B2 ， C1和C2坐标之间的关系.21. 阅读下列材料，并完成任务．筝形的定义：两组邻边分别相等的四边形叫做筝形，几何图形的定义通常可作为图形的性质也可以作为图形的判定方法.也就是说，如图，若四边形ABCD是一个筝形，则AB=AD，BC=CD；若AB=AD，BC=CD，则四边形ABCD是筝形.
如图，四边形ABCD是一个筝形，其中AB=AD，BC=CD．对角线AC，BD相交于点O，过点O作OM⊥AB，ON⊥AD，垂足分别为M，N.求证：四边形AMON是筝形.
22.(1)、如图1，将两个全等的三角板如图摆放，其中△ABC和ΔADE的直角顶点重合在点A处，∠ADE=∠ABC=60°，且点D在AC上，点B在AE上，∠C=∠E=30°，AB=AD，AC=AE，BC=DE，BC和DE相交于点F.求证：CF=EF.
(2)、如图2，将这两个三角板如图摆放，直角顶点A仍然重合，BC与DE相交于点F，AC与DE交于点M，AE和BC交于点N.猜想CF和EF还相等吗?说明理由.
(3)、如图3，在(2)的基础上，若∠DAM=30°.求证：线段DF和AC互相垂直平分.