山西省晋中市灵石县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 如图,点A的坐标(﹣1,2),点A关于y轴的对称点的坐标为( )
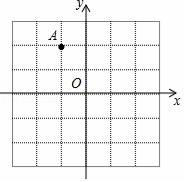 A、(1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(2,﹣1)3. 的平方根是( )A、 B、 C、 D、4. 回顾学习函数的过程,由函数的表达式通过列表、描点、连线画出函数的图象,再利用函数图象研究函数的性质.这个过程中主要体现的数学方法是( )A、数形结合 B、类比 C、公理化 D、归纳5. 与无理数 最接近的整数是( )A、4 B、5 C、6 D、76. 下列各点在一次函数y=2x﹣3的图象上的是( )A、(2,3) B、(2,1) C、(0,3) D、(3,07. 将一块体积为1000cm3的正方体锯成8块同样大小的小正方体木块,则每个小正方体木块的棱长为( )A、5cm B、6cm C、7cm D、8cm8. 一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )A、
A、(1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(2,﹣1)3. 的平方根是( )A、 B、 C、 D、4. 回顾学习函数的过程,由函数的表达式通过列表、描点、连线画出函数的图象,再利用函数图象研究函数的性质.这个过程中主要体现的数学方法是( )A、数形结合 B、类比 C、公理化 D、归纳5. 与无理数 最接近的整数是( )A、4 B、5 C、6 D、76. 下列各点在一次函数y=2x﹣3的图象上的是( )A、(2,3) B、(2,1) C、(0,3) D、(3,07. 将一块体积为1000cm3的正方体锯成8块同样大小的小正方体木块,则每个小正方体木块的棱长为( )A、5cm B、6cm C、7cm D、8cm8. 一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )A、 B、
B、 C、
C、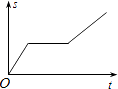 D、
D、 9. 中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(3,﹣2),则“兵”位于点( )
9. 中国象棋是中华民族的文化瑰宝,它源远流长,趣味性强,成为极其广泛的棋艺活动.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(3,﹣2),则“兵”位于点( ) A、(﹣1,1) B、(﹣2,﹣1) C、(﹣3,1) D、(﹣2,1)10. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米;其中正确的结论有( )
A、(﹣1,1) B、(﹣2,﹣1) C、(﹣3,1) D、(﹣2,1)10. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米;其中正确的结论有( )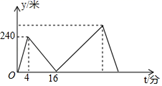 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在函数y=2x中,y的值随x值的增大而 . (填“增大”或“减小”)12. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为 ,到 轴的距离为 ,则点M的坐标是.13. 如图,在Rt△ABC中,AB=BC=1,∠ABC=90°,点A,B在数轴上对应的数分别为1,2.以点A为圈心,AC长为半径画弧,交数轴的负半轴于点D,则与点D对应的数是 .
 14. 在同一平面直角坐标系中,一次函数y=k1x+2(k1<0)与y=k2x+6(k2>0)的图象的交点在第象限.15. 如图,已知a,b,c分别是Rt△ABC的三条边长,∠C=90°,我们把关于x的形如y= 的一次函数称为“勾股一次函数”,若点P(1, )在“勾股一次函数”的图象上,且Rt△ABC的面积是5,则c的值是 .
14. 在同一平面直角坐标系中,一次函数y=k1x+2(k1<0)与y=k2x+6(k2>0)的图象的交点在第象限.15. 如图,已知a,b,c分别是Rt△ABC的三条边长,∠C=90°,我们把关于x的形如y= 的一次函数称为“勾股一次函数”,若点P(1, )在“勾股一次函数”的图象上,且Rt△ABC的面积是5,则c的值是 .
三、解答题
-
16. 计算(1)、(2)、(3+ )( ﹣2)(3)、( + ﹣ )÷17. 交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度,所用的经验公式是v=16 ,其中v表示车速(单位:km/h),d表示刹车后车轮滑过的距离(单位:m),f表示摩擦因数.在某次交通事故中,测得d=6m,f=1.5,求肇事汽车的车速.18. 如图,在四边形ABCD中,∠D=90°,AB=15,BC=20,CD=7,AD=24.
 (1)、求对角线AC的长;(2)、求四边形ABCD的面积.19. 2016年5月27日,太原与大同之间开通了“点对点”的云冈号旅游列车(中间不停车),该列车为空调车,由6节硬座车厢、1节软卧车厢、1节硬卧车厢组成.行驶的路程约300km,该旅游列车从太原站出发,以平均速度110km/h开往大同.用x(h)表示列车行驶的时间,y(km)表示列车距大同的距离.
(1)、求对角线AC的长;(2)、求四边形ABCD的面积.19. 2016年5月27日,太原与大同之间开通了“点对点”的云冈号旅游列车(中间不停车),该列车为空调车,由6节硬座车厢、1节软卧车厢、1节硬卧车厢组成.行驶的路程约300km,该旅游列车从太原站出发,以平均速度110km/h开往大同.用x(h)表示列车行驶的时间,y(km)表示列车距大同的距离. (1)、写出y与x之间的函数关系式;(2)、当该旅游列车距大同就还有80km时,求行驶了多长时间.20. 如图,在△ABC中,AB=AC=6,BC=4.以点B为坐标原点,BC所在的直线为x轴建立平面直角坐标系.
(1)、写出y与x之间的函数关系式;(2)、当该旅游列车距大同就还有80km时,求行驶了多长时间.20. 如图,在△ABC中,AB=AC=6,BC=4.以点B为坐标原点,BC所在的直线为x轴建立平面直角坐标系. (1)、请在图中画出符合条件的直角坐标系;(2)、求点A的坐标.21. 在12世纪印度数学家婆什迦罗的著作中,有一首诗,也称“荷花问题”:
(1)、请在图中画出符合条件的直角坐标系;(2)、求点A的坐标.21. 在12世纪印度数学家婆什迦罗的著作中,有一首诗,也称“荷花问题”:平平湖水清可鉴,面上半尺生荷花;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅”
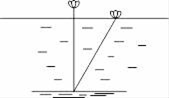
这首诗的大意是:在平静的湖面上,有一朵荷花高出水面半尺,忽然一阵强风吹来把荷花垂直拉到水里且荷花恰好落在水面.此时,捕鱼的人发现,花在水平方向上离开原来的位置2尺远,求湖水的深度.
 22. 阅读材料:
22. 阅读材料:小明在学习二次根式的化简后,遇到了这样一个需要化简的式子: .该如何化简呢?思考后,他发现3+2 =1+2 +( )2=(1+ )2 . 于是 = =1+ .善于思考的小明继续深入探索;当a+b =(m+n )2时(其中a,b,m,n均为正整数),则a+b =m2+2 mn+2n2 . 此时,a=m2+2n2 , b=2mn,于是, =m+n .请你仿照小明的方法探索并解决下列问题:
(1)、设a,b,m,n均为正整数且 =m+n ,用含m,n的式子分别表示a,b时,结果是a= , b=;(2)、利用(1)中的结论,选择一组正整数填空: =( )+( ) ;(3)、化简: .23. 如图,直线l:y=﹣ x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.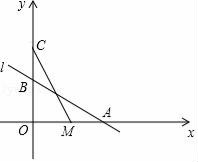 (1)、求点A的坐标;(2)、请从A,B两题中任选一题作答.
(1)、求点A的坐标;(2)、请从A,B两题中任选一题作答.A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.