河北省唐山市滦州市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
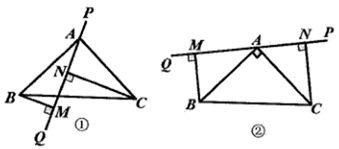
1. 若分式 有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列命题的逆命题为真命题的是( )A、全等三角形的对应角相等 B、如果 ,那么 C、对顶角相等 D、如果 ,那么3. 下列各式中正确的是( )A、 B、 C、 D、4. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )

A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD5. 若把分式 ( 均不为0)中的x和y都扩大3倍,则原分式的值是( )A、扩大3倍 B、缩小至原来的 C、不变 D、缩小至原来的6. 一个自然数的一个平方根是a,则与它相邻的下一个自然数的平方根是( )A、 B、 C、 D、7. 在某次数学小测中,老师给出了5个判断题.如图为张晓亮的答卷,每个小题判断正确得20分,他的得分应是( ) A、100分 B、80分 C、60分 D、40分8. 若关于x的方程 有增根,则k的值为( ).
A、100分 B、80分 C、60分 D、40分8. 若关于x的方程 有增根,则k的值为( ).
A、3 B、1 C、0 D、-19. 甲队修路120 m与乙队修路100 m所用天数相同,已知甲队比乙队每天多修10 m,设甲队每天修路xm.依题意,下面所列方程正确的是( )A、 B、 C、 D、10. 如图,在 中, , 分别是 上的点,且 .若 ,则 的度数为( )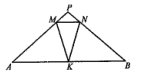 A、88° B、100° C、92° D、136°
A、88° B、100° C、92° D、136°二、填空题
-
11. 比较大小: .12. 若分式 的值为0,则 的值为.13. 用直尺和圆规作一个角等于已知角的示意图如下,则要说明 ,需要说明 ,则这两个三角形全等的依据是.(写出全等的简写)
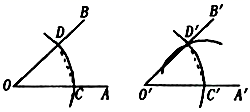 14. 若 ,则 .15. 已知 的平方根是 ,则 的立方根是.16. 当a=时,关于x的方程 的根是1.17. 若 =3-x,则x的取值范围是 .18. 一项工程甲独做需要m天完成,乙独做需要n天完成,那么甲、乙合作需要天完成.19. 在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=cm.
14. 若 ,则 .15. 已知 的平方根是 ,则 的立方根是.16. 当a=时,关于x的方程 的根是1.17. 若 =3-x,则x的取值范围是 .18. 一项工程甲独做需要m天完成,乙独做需要n天完成,那么甲、乙合作需要天完成.19. 在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=cm. 20. 计算: .
20. 计算: .三、解答题
-
21. 化简,再求值
,若x是满足 的整数,请选择一个合适的数求分式的值.
22. 已知:如图, , , .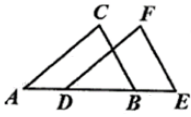
求证: .
23.(1)、用“<”、“>”或“=”填空: , ;(2)、由以上可知:① ;② ;(3)、计算: .(结果保留根号)24. 某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.(1)、求这个工程队原计划每天修建道路多少米?(2)、在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?