河北省唐山市路南区2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-25 类型：期中考试

进入出卷网下载

一、单选题

1. 已知a与b互为相反数，则 $b^{2} - a^{2}$ 的值为（）

A、0 B、1 C、 $- 1$ D、2

查看试题解析
2. 下列说法正确的是（）

A、形状相同的两个图形一定全等 B、两个长方形是全等图形 C、两个全等图形面积一定相等 D、两个正方形一定是全等图形

查看试题解析
3. 长为下列各组数中的三条线段能组成三角形的是（）

A、3，4，8 B、9，8，17 C、5，6，10 D、7，14，7

查看试题解析
4. 一个多边形的内角和是外角和的2倍，这个多边形是（）

A、四边形 B、五边形 C、六边形 D、八边形

查看试题解析
5. 下列运算正确的是（）

A、 $3 a^{3} - 2 a^{2} = a$ B、 $- {(2 a)}^{2} = - 4 a^{2}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 $a b \cdot 2 a b \cdot (- 3 a b^{2}) = a b (2 a b - 3 b)$

查看试题解析
6. 将一个四边形截去一个角后，它不可能是（）

A、六边形 B、五边形 C、四边形 D、三角形

查看试题解析
7. 如图，在方格纸.以AB为一边作△ABP，使之与△ABC全等，从P₁ ， P₂ ， P₃ ， P₄四个点中找出符合条件的点P，则点P有（）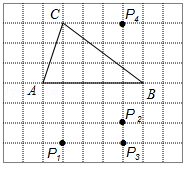

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 若 $2^{n} + 2^{n} + 2^{n} + 2^{n} = 4$ ，则n=（）

A、4 B、2 C、1 D、0

查看试题解析
9. 如图， $△ A C E ≌ △ D B F$ ， $A E / / D F$ ， $A B = 3$ ， $B C = 2$ ，则 $A D$ 的长度等于（）

A、2 B、8 C、6 D、3

查看试题解析
10. 如图，若干个全等的正五边形排成环状，图中所示的是前3个正五边形，要完成这一圆环还需正五边形的个数为（）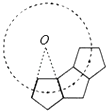

A、10 B、9 C、8 D、7

查看试题解析
11. 下列各式，能够表示图中阴影部分的面积的是（　　）
①ac+（b﹣c）c；②ac+bc﹣c²；③ab﹣（a﹣c）（b﹣c）；④（a﹣c）c+（b﹣c）c+c²

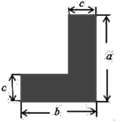A、①②③④ B、①②③ C、①② D、①

查看试题解析
12. 如图，已知四边形ABCD.AB∥DC，连接 BD，BE 平分∠ABD，BE⊥AD，∠EBC 和∠DCB 的角平分线相交于点F，若∠ADC=110°，则∠F 的度数为（）.

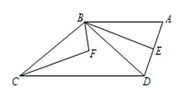A、115° B、110° C、105° D、100°

查看试题解析

二、填空题

13. 计算： ${(- 3 a^{3} b)}^{2} \div a^{4} b^{3} =$ ．

查看试题解析
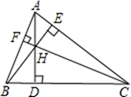
14. 若 $4 x^{2} + m x + 9$ 是一个完全平方式，则m的值是．

查看试题解析
15. 如图，H若是 $Δ A B C$ 三条高 $A D$ ， $B E$ ， $C F$ 的交点，则 $Δ B H A$ 中边 $B H$ 上的高是.（用已知的字母表示）

查看试题解析
16. 若 $a + b = 2$ ， $a b = 3$ ，则代数式 $a^{3} b + 2 a^{2} b^{2} + a b^{3}$ 的值为．

查看试题解析
17. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D F ⊥ A B$ ，垂足为F， $D E = D G$ ， $△ A D G$ 和 $△ A E D$ 的面积分别为52和36，则 $△ E D F$ 的面积为．

查看试题解析
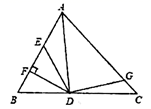18. 观察下列各式：
$1^{2} + 3^{2} + 4^{2} = 2 \times (1^{2} + 3^{2} + 3)$

$2^{2} + 3^{2} + 5^{2} = 2 \times (2^{2} + 3^{2} + 6)$

$3^{2} + 6^{2} + 9^{2} = 2 \times (3^{2} + 6^{2} + 18)$

$\cdot \cdot \cdot \cdot \cdot \cdot$

若a，b表示等式左边的由小到大的前两个底数，请用字母a，b表示你发现的等式为．

查看试题解析

三、解答题

19. 利用乘法公式有时能进行简便计算．
例： $101 \times 99 = (100 + 1) (100 - 1) = 100^{2} - 1^{2} = 10000 - 1 = 9999$ ．

请参考给出的例题，通过简便方法计算：

(1)、 $2002 \times 1998$ ；

(2)、 $86 \times 3.14 + 34 \times 3.14 - 20 \times 3.14$ ；

查看试题解析
20.

(1)、因式分解： $9 a^{2} (x - y) - b^{2} (x - y)$ ．

(2)、解方程： $(x + 3) (x - 5) - (x + 1) (x - 1) = 2$ ．

查看试题解析
21. 如图，在 $△ A B C$ . $A E$ 是 $∠ B A C$ 的平分线， $A D$ 是 $B C$ 边上的高， $∠ B A C = 80 °$ ， $∠ E A D = 15 °$ ，求 $∠ B$ 的度数．

查看试题解析
22. 若 $(x^{2} + m x) (x^{2} - 3 x + n)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 项，求m和n的值．

查看试题解析
23. 如图． $A D$ 平分 $∠ B A C$ ， $D E ⊥ A C$ ，垂足为E， $B F ∥ A C$ 交 $E D$ 的延长线于点F，若 $B C$ 恰好平分 $∠ A B F$ ．求证：

(1)、点D为 $E F$ 的中点；

(2)、 $A D ⊥ B C$ ．

查看试题解析
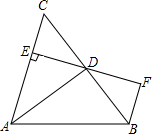24. 如图，将一张长方形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小长方形，且m>n.(以上长度单位：cm)

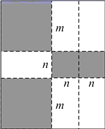(1)、观察图形，可以发现代数式2m²＋5mn＋2n²可以因式分解为；

(2)、若每块小长方形的面积为10 cm² ，四个正方形的面积和为58 cm² ，试求图中所有裁剪线(虚线部分)长之和.

查看试题解析
25. 如图（1）， $A B = 8 c m$ ， $A C ⊥ A B$ ， $B D ⊥ A B$ ， $A C = B D = 6 c m$ ．点P在线段 $A B$ 上以 $2 c m / s$ 的速度由点A向点B运动，同时，点Q在线段 $B D$ 上由点B向点D运动，它们运动的时间为 $t (s)$

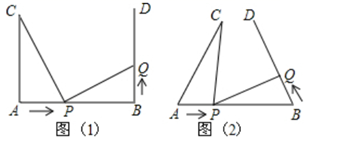(1)、若点Q的运动速度与点P的运动速度相等，当 $t = 1$ 时，判断线段 $P C$ 与 $P Q$ 满足的关系，并说明理由；

(2)、如图（2），将图（1）中的“ $A C ⊥ A B$ ， $B D ⊥ A B$ ”为改“ $∠ C A B = ∠ D B A = α °$ ”，其它条件不变．设点Q的运动速度为 $x c m / s$ ，是否存在实数x，使得 $△ A C P$ 与 $△ B P Q$ 全等？若存在，求出相应的x、t的值；若不存在，请说明理由．

查看试题解析