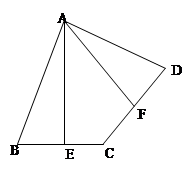河北省唐山市丰南区2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 下列四个图案中,不是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( )
2. 如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( ) A、30° B、40° C、50° D、60°3. 已知等腰三角形的两边长是5cm和10cm,则它的周长是( )A、21cm B、25cm C、20cm D、20cm或25cm4. 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A、30° B、40° C、50° D、60°3. 已知等腰三角形的两边长是5cm和10cm,则它的周长是( )A、21cm B、25cm C、20cm D、20cm或25cm4. 如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( ) A、120° B、115° C、110° D、105°5. 如图, ≌ , , ,则 的度数为( ).
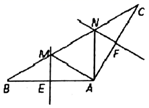
A、120° B、115° C、110° D、105°5. 如图, ≌ , , ,则 的度数为( ).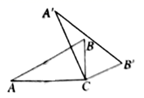 A、 B、 C、 D、6. 若从一多边形的一个顶点出发,最多可引10条对角线,则它是( )A、十三边形 B、十二边形 C、十一边形 D、十边形7. 如图,若 是等边三角形, , 是 的平分线,延长 到E,使 ,则 的长为( ).
A、 B、 C、 D、6. 若从一多边形的一个顶点出发,最多可引10条对角线,则它是( )A、十三边形 B、十二边形 C、十一边形 D、十边形7. 如图,若 是等边三角形, , 是 的平分线,延长 到E,使 ,则 的长为( ).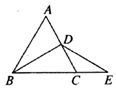 A、6 B、7 C、8 D、98. 如图, , , ≌ , 与 交于点D.若 , ,则 的面积为( ).
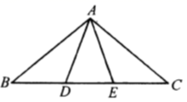
A、6 B、7 C、8 D、98. 如图, , , ≌ , 与 交于点D.若 , ,则 的面积为( ).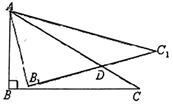 A、6 B、12 C、18 D、369. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC点E,AC的长为12cm,则△BCE的周长等于( )
A、6 B、12 C、18 D、369. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC点E,AC的长为12cm,则△BCE的周长等于( ) A、16cm B、20cm C、24cm D、26cm10. 如图, 的度数为( ).
A、16cm B、20cm C、24cm D、26cm10. 如图, 的度数为( ).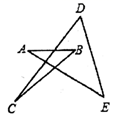 A、 B、 C、 D、11. 如图, 中,以B为圆心, 长为半径画弧,分别交 , 于D,E两点,并连接 , .若 , ,则 的度数为( ).
A、 B、 C、 D、11. 如图, 中,以B为圆心, 长为半径画弧,分别交 , 于D,E两点,并连接 , .若 , ,则 的度数为( ). A、 B、 C、 D、12. 将一副三角板按如图所示方式叠放在一起,若 ,则阴影部分的面积是( ).
A、 B、 C、 D、12. 将一副三角板按如图所示方式叠放在一起,若 ,则阴影部分的面积是( ).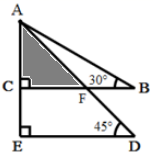 A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14二、填空题
-
13. 在平面直角坐标系中,点 与点 关于x轴对称,则 的值是 .14. 如图,已知AB=BD,∠A=∠D若直接应用“SAS”判定△ABC≌△DBE,则需要添加的一个条件 是.
 15. 如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字的格子内.
15. 如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字的格子内.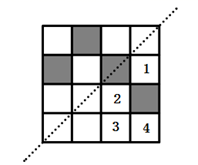 16. 如图, 中, , ,则 的度数是 .
16. 如图, 中, , ,则 的度数是 . 17. 如图,正三角形的三个内角平分线交于O点,则 .
17. 如图,正三角形的三个内角平分线交于O点,则 . 18. 三个全等三角形按如图的形式摆放,若∠1=88°,则∠2+∠3=°.
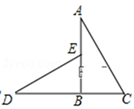
18. 三个全等三角形按如图的形式摆放,若∠1=88°,则∠2+∠3=°. 19. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是 .
19. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是 . 20. 已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为 .
20. 已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为 .
三、解答题
-
21.(1)、已知 中, , , 是 的角平分线,求 的度数.
 (2)、已知:如图, , , , .求证: .
(2)、已知:如图, , , , .求证: . 22. 如图,在 中, , , , 、 交于点O.求证:
22. 如图,在 中, , , , 、 交于点O.求证: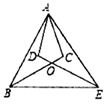 (1)、 ;(2)、 .
(1)、 ;(2)、 .