河北省石家庄市高邑县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 如果分式 有意义,那么x的取值范围是( )A、 B、 C、 D、 或2. 在 , , , 这四个数中,绝对值最小的数是( )A、 B、 C、 D、3. 的算术平方根是( )
A、3 B、 C、±3 D、±4. 在实数 , ,π﹣2, ,0.121 221 222 1…(两个”1”之间依次多一个“2”)中,有理数有( )A、1个 B、2个 C、3个 D、4个5. 化简: 的结果是( )A、 B、 C、 D、6. 根据以下条件:①已知三边;②已知两边及其夹角;③已知两角及其夹边;④已知两边及其中一边的对角 利用尺规作图能用尺规作出唯一的三角形有( )A、①② B、①③ C、①②③ D、①②④7. 龙华区某校改造过程中,需要整修校门口一段全长2400m的道路,为了保证开学前师生进出不受影响,实际工作效率比原计划提高了 ,结果提前8天完成任务,若设原计划每天整个道路x米,根据题意可得方程( )A、 B、 C、 D、8. 下列命题的逆命题不成立的是( )A、两直线平行,同旁内角互补 B、如果两个实数相等,那么它们的平方相等 C、平行四边形的对角线互相平分 D、全等三角形的对应边相等9. 如图,D、E分别是△ABC的边AC、BC上的点,且△ADB≌△EDB≌△EDC , 则∠C的度数为( ) A、15º B、20º C、25º D、30º10. 如图,△ABC≌△EFD且 AB=EF,CE=3.5,CD=3,则 AC=( )
A、15º B、20º C、25º D、30º10. 如图,△ABC≌△EFD且 AB=EF,CE=3.5,CD=3,则 AC=( ) A、6.5 B、3.5 C、3 D、511. 已知 的整数部分为 , 的小数部分为b,则a+b的值为( )A、10 B、 C、 D、12. 如图,在矩形 中无重叠放入面积为16和12的两张正方形纸片,则图中空白部分的面积为( )
A、6.5 B、3.5 C、3 D、511. 已知 的整数部分为 , 的小数部分为b,则a+b的值为( )A、10 B、 C、 D、12. 如图,在矩形 中无重叠放入面积为16和12的两张正方形纸片,则图中空白部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 当a=时, 的值为零.14. 已知 + =0,则(a﹣b)2的平方根是 .15. 直角三角形两锐角互余的逆命题是.16. 已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为(填序号)
①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
②作直线 ,在 上截取 ;
③连接 , , 为所求作的三角形.
 17. 小明是一个电脑爱好者,他设计了一个程序,如图.当输入x的值是64时,输出的y值是.
17. 小明是一个电脑爱好者,他设计了一个程序,如图.当输入x的值是64时,输出的y值是. 18. 甲、乙两人站在一条道路的两端同时出发相向而行,1.2小时相遇,若甲走完这条道路需2小时,则乙走完这条路需小时。19. 定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,那么:(3+2i)(3-2i)= .20. 定义新运算“⊕”如下,当 时, ,当 时, ;则 的值为.
18. 甲、乙两人站在一条道路的两端同时出发相向而行,1.2小时相遇,若甲走完这条道路需2小时,则乙走完这条路需小时。19. 定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,那么:(3+2i)(3-2i)= .20. 定义新运算“⊕”如下,当 时, ,当 时, ;则 的值为.三、解答题
-
21. 本学期学习了分式方程的解法,下面是晶晶同学的解题过程:
解方程
解:整理,得: …………………………第①步
去分母,得: …………………………第②步
移项,得: ……………………… 第③步
合并同类项,得: ……………………… 第④步
系数化1,得: …………………………第⑤步
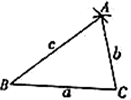
检验:当 时,
所以原方程的解是 . ………………………第⑥步
上述晶晶的解题过程从第步开始出现不符合题意,错误的原因是 . 请你帮晶晶改正不符合题意,写出完整的解题过程.
22. 如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径. (1)、把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是数(填“无理”或“有理”),这个数是;(2)、把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是;(3)、圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,-5,+4,+3,-2当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?23. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 ,点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
(1)、把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是数(填“无理”或“有理”),这个数是;(2)、把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是;(3)、圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,-5,+4,+3,-2当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?23. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 ,点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.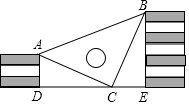 24. 随着我国经济的发展,高铁逐渐成为了主要的交通工具,一般的高铁G字头的高速动车组以D字头的动车组,由大连到北京的G377的平均速度是D31的平均速度的 倍,行驶相同的路程 千米,G377少用 个小时。(1)、求D31的平均速度。(2)、若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式,现阶段D31票价为 元/张,G377票件为 元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?25. 如图,已知 中, , ,点 为 的中点,如果点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动.
24. 随着我国经济的发展,高铁逐渐成为了主要的交通工具,一般的高铁G字头的高速动车组以D字头的动车组,由大连到北京的G377的平均速度是D31的平均速度的 倍,行驶相同的路程 千米,G377少用 个小时。(1)、求D31的平均速度。(2)、若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式,现阶段D31票价为 元/张,G377票件为 元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?25. 如图,已知 中, , ,点 为 的中点,如果点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动. (1)、若点 与点 的运动速度相等,经过1秒后, 与 是否全等?请说明理由;(2)、若点 与点 的运动速度不相等,当点 的运动速度为多少时,能使 与 全等?
(1)、若点 与点 的运动速度相等,经过1秒后, 与 是否全等?请说明理由;(2)、若点 与点 的运动速度不相等,当点 的运动速度为多少时,能使 与 全等?