河北省石家庄市28中教育集团2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 下列各图中,是轴对称图案的是( )A、
 B、
B、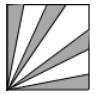 C、
C、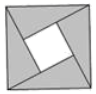 D、
D、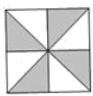 2. 在实数0.3,0, , ,0.123456…中,无理数的个数是( )A、2 B、3 C、4 D、53. 若分式 的值为0,则x的值为( )A、﹣1 B、0 C、2 D、﹣1或24. 下列说法错误的是( )A、4的算术平方根是2 B、 的平方根是 C、8的立方根是 D、0的平方根是05. 下列式子一定是二次根式的是( )A、 B、 C、 D、6. 已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
2. 在实数0.3,0, , ,0.123456…中,无理数的个数是( )A、2 B、3 C、4 D、53. 若分式 的值为0,则x的值为( )A、﹣1 B、0 C、2 D、﹣1或24. 下列说法错误的是( )A、4的算术平方根是2 B、 的平方根是 C、8的立方根是 D、0的平方根是05. 下列式子一定是二次根式的是( )A、 B、 C、 D、6. 已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )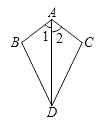 A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA7. A、B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为5千米/时.若设该轮船在静水中的速度为x千米/时,则可列方程( )A、 B、 C、 D、8. 下列式子为最简二次根式的是( )
A、AB=AC B、BD=CD C、∠B=∠C D、∠BDA=∠CDA7. A、B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为5千米/时.若设该轮船在静水中的速度为x千米/时,则可列方程( )A、 B、 C、 D、8. 下列式子为最简二次根式的是( )
A、 B、 C、 D、9. 下列二次根式计算正确的是( )A、 B、 C、 D、10. 如图,已知 , , .若 , ,则 的长为( )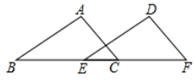 A、4 B、3.5 C、3 D、2.511. 如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )
A、4 B、3.5 C、3 D、2.511. 如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )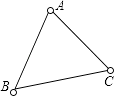 A、三条边的垂直平分线的交点 B、三个角的角平分线的交点 C、三角形三条高的交点 D、三角形三条中线的交点12. 已知:m、n为两个连续的整数,且 ,以下判断正确的是( )A、 B、 的小数部分是0.236 C、 的整数部分与小数部分的差是 D、13. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A、三条边的垂直平分线的交点 B、三个角的角平分线的交点 C、三角形三条高的交点 D、三角形三条中线的交点12. 已知:m、n为两个连续的整数,且 ,以下判断正确的是( )A、 B、 的小数部分是0.236 C、 的整数部分与小数部分的差是 D、13. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )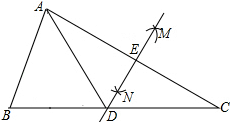 A、16cm B、19cm C、22cm D、25cm14. 已知正方体A的体积是棱长为 的正方体B的体积的 ,则正方体A的棱长是( )A、 B、 C、 D、15. 化简 的结果为( )A、 B、2 C、 D、16. 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌△CDE,②△ABD和△ACD的面积相等,③BF∥CE,④∠DEC=70°,其中正确的有( )
A、16cm B、19cm C、22cm D、25cm14. 已知正方体A的体积是棱长为 的正方体B的体积的 ,则正方体A的棱长是( )A、 B、 C、 D、15. 化简 的结果为( )A、 B、2 C、 D、16. 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌△CDE,②△ABD和△ACD的面积相等,③BF∥CE,④∠DEC=70°,其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
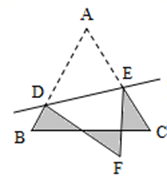
17. , , 的倒数是.18. “350亿”这个数用科学记数法表示为;用四舍五入法将130.96精确到十分位是.19. 比较大小: 1.20. 如图,等边 的边长为 ,D、E分别是 、 上的点,将 沿直线 折叠,点A落在点F处,且点F在 外部,则阴影部分图形的周长为cm.
三、解答题
-
21. 计算:(1)、(2)、(3)、(4)、22. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为 .现已知 的三边长为 , , ,求 的面积.23. 在 的方格纸中, 的三个顶点都在格点上,
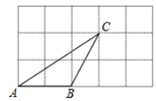 (1)、在图中画出线段 ,使 ,其中 是格点.(2)、根据确定的 的位置,证明 .24.(1)、先化简,再求值: ,其中(2)、先化简,再求值: ,25. 如图是由边长为1的小正方形组成的 网格,直线 是一条网格线,点E,F在格点上, 的三个顶点都在格点(网格线的交点)上.
(1)、在图中画出线段 ,使 ,其中 是格点.(2)、根据确定的 的位置,证明 .24.(1)、先化简,再求值: ,其中(2)、先化简,再求值: ,25. 如图是由边长为1的小正方形组成的 网格,直线 是一条网格线,点E,F在格点上, 的三个顶点都在格点(网格线的交点)上.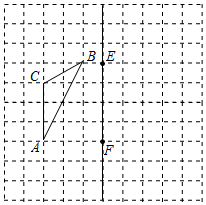
⑴作出 关于直线 对称的 ;
⑵在直线 上画出点M,使四边形 的周长最小;
⑶在这个 网格中,到点A和点B的距离相等的格点有几个.
26. 如果记 ,并且 表示当 时y的值,即 ; 表示当 时y的值,即 ; 表示当 时 的值,即 ;…(1)、计算下列各式的值:.
.
(2)、当n为正整数时,猜想 的结果并说明理由;(3)、求 的值.27. 乐乐和数学小组的同学们研究了如下问题,请你也来试一下吧.点 是直线 上一点,在同一平面内,乐乐他们把一个等腰直角三角板 任意放,其中直角顶点 与点 重合,过点 作直线 ,垂足为点 ,从过点 作 ,垂足为点 .
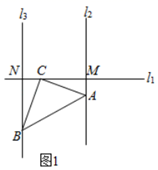
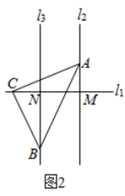
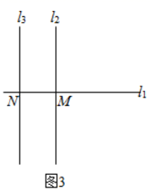 (1)、当直线 , 位于点 的异侧时,如图1,线段 , , 之间的数量关系(不必说明理由);(2)、当直线 , 位于点 的右侧时,如图2,判断线段 , , 之间的数量系,并说明理由;(3)、当直线 , 位于点 的左侧时,如图3,请你补全图形,并直接写出线段 , , 之间的数量关系.
(1)、当直线 , 位于点 的异侧时,如图1,线段 , , 之间的数量关系(不必说明理由);(2)、当直线 , 位于点 的右侧时,如图2,判断线段 , , 之间的数量系,并说明理由;(3)、当直线 , 位于点 的左侧时,如图3,请你补全图形,并直接写出线段 , , 之间的数量关系.