河北省邯郸市永年区2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-25 类型:期中考试
一、单选题
-
1. 表示( )A、3的平方根 B、3的立方根 C、3的算术平方根 D、3的一半2. 若 能使一个分式无意义,则这个分式可以是( )A、 B、 C、 D、3. 对于命题“如果∠1+∠2=90°,那么∠1=∠2”,能说明它是假命题的反例是( )A、∠1=60°,∠2=40° B、∠1=50°,∠2=40° C、∠1=∠2=40° D、∠1=∠2=45°4. 由四舍五入得到的近似数88.35万.精确到( )A、十分位 B、百分位 C、百位 D、十位5. 已知M表示一个整式,若 是最简分式,则M可以是( )A、 B、 C、 D、6. 工人师傅常用角尺平分一个任意角,具体做法如下:如图,已知 是一个任意角,在边 , 上分别取 ,移动角尺两边相同的刻度分别与点 、 重合,则过角尺顶点 的射线 便是 角平分线.在证明 时运用的判定定理是( )
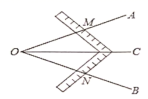 A、 B、 C、 D、7. 分式 与 的最简公分母是( )A、 B、 C、 D、8. 如图,若实数m=﹣ +1,则数轴上表示m的点应落在( )
A、 B、 C、 D、7. 分式 与 的最简公分母是( )A、 B、 C、 D、8. 如图,若实数m=﹣ +1,则数轴上表示m的点应落在( ) A、线段AB上 B、线段BC上 C、线段CD上 D、线段DE上9. 如图,一个体积为216cm3的魔方放在桌面上,桌面被覆盖的面积是( )
A、线段AB上 B、线段BC上 C、线段CD上 D、线段DE上9. 如图,一个体积为216cm3的魔方放在桌面上,桌面被覆盖的面积是( ) A、4cm2 B、16cm2 C、36cm2 D、64cm210. 下列说法,正确的是( )
A、4cm2 B、16cm2 C、36cm2 D、64cm210. 下列说法,正确的是( )① 是分数;② 是有理数;③ 是分数;④ 是无理数
A、①② B、①③ C、①④ D、②③11. 关于分式 ,下列说法正确的是( )A、分子、分母中的x、y均扩大3倍,分式的值也扩大3倍; B、分子、分母的中x扩大3倍,y不变,分式的值扩大3倍; C、分子、分母的中y扩大3倍,x不变,分式的值不变; D、分子、分母中的x、y均扩大3倍,分式的值不变;12. 如图是作 的作图痕迹,则此作图的已知条件是( )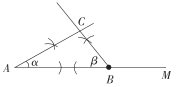 A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角13. 某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4000元,购买篮球用了2800元,篮球单价比足球贵16元.若可列方程 表示题中的等量关系,则方程中x表示的是( )A、足球的单价 B、篮球的单价 C、足球的数量 D、篮球的数量14. 如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌ ,△AEB≌ ,且 ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角13. 某校为进一步开展“阳光体育”活动,购买了一批篮球和足球.已知购买足球数量是篮球的2倍,购买足球用了4000元,购买篮球用了2800元,篮球单价比足球贵16元.若可列方程 表示题中的等量关系,则方程中x表示的是( )A、足球的单价 B、篮球的单价 C、足球的数量 D、篮球的数量14. 如图所示,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌ ,△AEB≌ ,且 ,BE、CD交于点F,若∠BAC=40°,则∠BFC的大小是( ) A、105° B、100° C、110° D、115°
A、105° B、100° C、110° D、115°二、填空题
-
15. 命题“如果两个数相等,那么它们的倒数相等”的逆命题是 .16. 已知 和 是一个正数两个不相等的平方根,则m=;这个正数的平方根是 .17. 若关于x的方程 有增根,则m= , 若关于x的方程 的解是负数,则m的取值范围是 .
三、解答题
-
18. 比较 与 的大小,并写出你的判断过程.19. 小明解方程 =3出现了不符合题意,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)、小明解答过程是从第步开始出错的,原方程化为第一步的根据是 .(2)、请写出此题正确的解答过程.20. 某小区有一块长方形草坪,为了加强保护,小区管理人员准备用篱笆沿草坪边缘将其围起来,已知该长方形草坪的长是宽的4倍,草坪的面积是 .求所需篱笆的总长度.21. 化简求值: ,其中 .22. 已知: , , , ,垂足分别为D,E,(1)、如图1,
①线段 和 的数量关系是;
②请写出线段 , , 之间的数量关系并证明.
(2)、如图2,若已知条件不变,上述结论②还成立吗?如果不成立,请直接写出线段 , , 之间的数量关系. 23. 甲、乙两名采购员同去一家饲料公司购买两次饲料.两次饲料的价格分别为m元/千克和n元/千克(m、n都为正数,且 ),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.(1)、用含m、n的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?(2)、若规定:谁两次购买饲料的平均单价低,谁的购货方式合算,请你判断甲、乙两名采购员购货方式哪个更合算?说明理由.24. 如图(1),在 和 中, 为 边 上一点, 平分 , , .
23. 甲、乙两名采购员同去一家饲料公司购买两次饲料.两次饲料的价格分别为m元/千克和n元/千克(m、n都为正数,且 ),两名采购员的购货方式不同,其中甲每次购买800千克;乙每次用去800元,而不管购买多少饲料.(1)、用含m、n的代数式表示甲、乙两名采购员两次购买饲料的平均单价各是多少?(2)、若规定:谁两次购买饲料的平均单价低,谁的购货方式合算,请你判断甲、乙两名采购员购货方式哪个更合算?说明理由.24. 如图(1),在 和 中, 为 边 上一点, 平分 , , . (1)、求证:(2)、如图(2),若 ,连接 交 于 , 为边 上一点,满足 ,连接 交 于 . ①求 的度数;
(1)、求证:(2)、如图(2),若 ,连接 交 于 , 为边 上一点,满足 ,连接 交 于 . ①求 的度数;②若 平分 ,试说明: 平分 .