黑龙江省大庆市2020年中考数学试卷
试卷更新日期:2020-09-23 类型:中考真卷
一、单选题
-
1. -1,0, , 这四个数中,最大的数是( )A、-1 B、0 C、 D、2. 天王星围绕太阳公转的轨道半径长约为 ,数字2 900 000 000用科学记数法表示为( )A、 B、 C、 D、3. 若 ,则 的值为( )A、-5 B、5 C、1 D、-14. 函数 的自变量 的取值范围是( )A、 B、 C、 D、5. 已知正比例函数 和反比例函数 ,在同一直角坐标系下的图象如图所示,其中符合 的是( )
 A、①② B、①④ C、②③ D、③④6. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与数字5所在的面相对的面上标的数字为( )
A、①② B、①④ C、②③ D、③④6. 将正方体的表面沿某些棱剪开,展成如图所示的平面图形,则原正方体中与数字5所在的面相对的面上标的数字为( ) A、1 B、2 C、3 D、47. 在一次青年歌手比赛中,七位评委为某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0(单位:分).若去掉一个最高分和一个最低分,则去掉前与去掉后没有改变的一个统计量是( )A、平均分 B、方差 C、中位数 D、极差8. 底面半径相等的圆锥与圆柱的高的比为1:3,则圆锥与圆柱的体积的比为( )A、1:1 B、1:3 C、1:6 D、1:99. 已知两个直角三角形的三边长分别为3,4, 和6,8, ,且这两个直角三角形不相似,则 的值为( )A、 或 B、15 C、 D、10. 如图,在边长为2的正方形 中, , 分别为 与 的中点,一个三角形 沿竖直方向向上平移,在运动的过程中,点 恒在直线 上,当点 运动到线段 的中点时,点 , 恰与 , 两边的中点重合.设点 到 的距离为 ,三角形 与正方形 的公共部分的面积为 ,则当 时, 的值为( )
A、1 B、2 C、3 D、47. 在一次青年歌手比赛中,七位评委为某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0(单位:分).若去掉一个最高分和一个最低分,则去掉前与去掉后没有改变的一个统计量是( )A、平均分 B、方差 C、中位数 D、极差8. 底面半径相等的圆锥与圆柱的高的比为1:3,则圆锥与圆柱的体积的比为( )A、1:1 B、1:3 C、1:6 D、1:99. 已知两个直角三角形的三边长分别为3,4, 和6,8, ,且这两个直角三角形不相似,则 的值为( )A、 或 B、15 C、 D、10. 如图,在边长为2的正方形 中, , 分别为 与 的中点,一个三角形 沿竖直方向向上平移,在运动的过程中,点 恒在直线 上,当点 运动到线段 的中点时,点 , 恰与 , 两边的中点重合.设点 到 的距离为 ,三角形 与正方形 的公共部分的面积为 ,则当 时, 的值为( )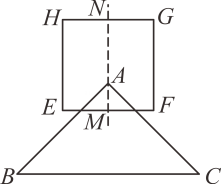 A、 或 B、 或 C、 D、 或
A、 或 B、 或 C、 D、 或二、填空题
-
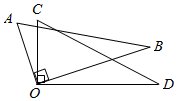
11. 点(2,3)关于y轴对称的点的坐标为 .12. 分解因式: =。13. 一个周长为 的三角形,由它的三条中位线构成的三角形的周长为 .14. 将两个三角尺的直角顶点重合为如图所示的位置,若 ,则 .
 15. 两个人做游戏:每个人都从-1,0,1这三个整数中随机选择一个写在纸上,则两人所写整数的绝对值相等的概率为 .16. 如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为 .
15. 两个人做游戏:每个人都从-1,0,1这三个整数中随机选择一个写在纸上,则两人所写整数的绝对值相等的概率为 .16. 如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为 . 17. 已知关于 的一元二次方程 ,有下列结论:
17. 已知关于 的一元二次方程 ,有下列结论:①当 时,方程有两个不相等的实根;
②当 时,方程不可能有两个异号的实根;
③当 时,方程的两个实根不可能都小于1;
④当 时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为 .
18. 如图,等边 中, ,点 ,点 分别是边 , 上的动点,且 ,连接 、 交于点 ,当点 从点 运动到点 时,则点 的运动路径的长度为 .
三、解答题
-
19. 计算:20. 先化简,再求值: ,其中 .21. 解方程:22. 如图, ,CD为两个建筑物,两建筑物底部之间的水平地面上有一点 .从建筑物 的顶点 测得 点的俯角为45°,从建筑物 的顶点 测得 点的俯角为75°,测得建筑物 的顶点 的俯角为30°.若已知建筑物 的高度为20米,求两建筑物顶点 、 之间的距离(结果精确到 ,参考数据: , )
 23. 为了了解某校某年级1000名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过150次),整理后绘制成如下的频数直方图,图中的 , 满足关系式 .后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.
23. 为了了解某校某年级1000名学生一分钟的跳绳次数,从中随机抽取了40名学生的一分钟跳绳次数(次数为整数,且最高次数不超过150次),整理后绘制成如下的频数直方图,图中的 , 满足关系式 .后由于保存不当,部分原始数据模糊不清,但已知缺失数据都大于120.请结合所给条件,回答下列问题.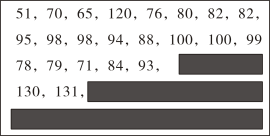
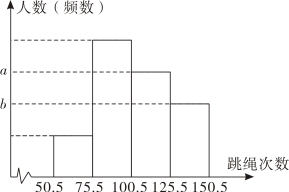 (1)、求问题中的总体和样本容量;(2)、求 , 的值(请写出必要的计算过程);(3)、如果一分钟跳绳次数在125次以上(不含125次)为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的人数大约是多少人?(注:该年级共1000名学生)24. 如图,在矩形 中, 为对角线 的中点,过点 作直线分别与矩形的边 , 交于 , 两点,连接 , .
(1)、求问题中的总体和样本容量;(2)、求 , 的值(请写出必要的计算过程);(3)、如果一分钟跳绳次数在125次以上(不含125次)为跳绳成绩优秀,那么估计该校该年级学生跳绳成绩优秀的人数大约是多少人?(注:该年级共1000名学生)24. 如图,在矩形 中, 为对角线 的中点,过点 作直线分别与矩形的边 , 交于 , 两点,连接 , .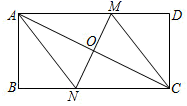 (1)、求证:四边形 为平行四边形;(2)、若 , ,且 ,求 的长25. 期中考试后,某班班主任对在期中考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,购买甲种笔记本15个,乙种笔记本20个,共花费250元.已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元.(1)、求购买一个甲种、一个乙种笔记本各需多少元?(2)、两种笔记本均受到了获奖同学的喜爱,班主任决定在期末考试后再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售.如果班主任此次购买甲、乙两种笔记本的总费用不超过上一次总费用的90%?至多需要购买多少个甲种笔记本?并求购买两种笔记本总费用的最大值.26. 如图,反比例函数 与一次函数 的图象在第二象限的交点为 ,在第四象限的交点为 ,直线 ( 为坐标原点)与函数 的图象交于另一点 .过点 作 轴的平行线,过点 作 轴的平行线,两直线相交于点 , 的面积为6.
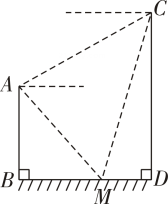
(1)、求证:四边形 为平行四边形;(2)、若 , ,且 ,求 的长25. 期中考试后,某班班主任对在期中考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,购买甲种笔记本15个,乙种笔记本20个,共花费250元.已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元.(1)、求购买一个甲种、一个乙种笔记本各需多少元?(2)、两种笔记本均受到了获奖同学的喜爱,班主任决定在期末考试后再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售.如果班主任此次购买甲、乙两种笔记本的总费用不超过上一次总费用的90%?至多需要购买多少个甲种笔记本?并求购买两种笔记本总费用的最大值.26. 如图,反比例函数 与一次函数 的图象在第二象限的交点为 ,在第四象限的交点为 ,直线 ( 为坐标原点)与函数 的图象交于另一点 .过点 作 轴的平行线,过点 作 轴的平行线,两直线相交于点 , 的面积为6.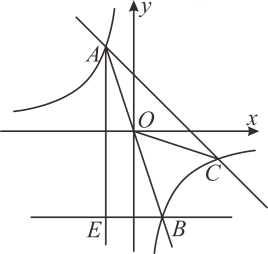 (1)、求反比例函数 的表达式;(2)、求点 , 的坐标和 的面积.27. 如图,在 中, ,以 为直径的 交 于点 ,连接 ,过点 作 ,垂足为 , 、 的延长线交于点 .
(1)、求反比例函数 的表达式;(2)、求点 , 的坐标和 的面积.27. 如图,在 中, ,以 为直径的 交 于点 ,连接 ,过点 作 ,垂足为 , 、 的延长线交于点 . (1)、求证: 是 的切线;(2)、求证: ;(3)、若 , ,求 的长.28. 如图,抛物线 与 轴交于 , 两点( 在 的右侧),且经过点 和点 .
(1)、求证: 是 的切线;(2)、求证: ;(3)、若 , ,求 的长.28. 如图,抛物线 与 轴交于 , 两点( 在 的右侧),且经过点 和点 . (1)、求抛物线的函数表达式;(2)、连接 ,经过点 的直线 与线段 交于点 ,与抛物线交于另一点 .连接 , , , 的面积与 的面积之比为1:7.点 为直线 上方抛物线上的一个动点,设点 的横坐标为 .当 为何值时, 的面积最大?并求出最大值;(3)、在抛物线 上,当 时, 的取值范围是 ,求 的取值范围.(直接写出结果即可)
(1)、求抛物线的函数表达式;(2)、连接 ,经过点 的直线 与线段 交于点 ,与抛物线交于另一点 .连接 , , , 的面积与 的面积之比为1:7.点 为直线 上方抛物线上的一个动点,设点 的横坐标为 .当 为何值时, 的面积最大?并求出最大值;(3)、在抛物线 上,当 时, 的取值范围是 ,求 的取值范围.(直接写出结果即可)