天津市南开区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-23 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,与点(4,﹣5)关于原点对称的点的坐标是( )A、(﹣4,﹣5) B、(﹣4,5) C、(4,﹣5) D、(4,5)2. 下列手机手势解锁图案中,是中心对称图形的是( )A、
 B、
B、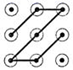 C、
C、 D、
D、 3. 已知关于 的方程 ,下列说法正确的是( )A、当 时,方程无解 B、当 时,方程有一个实数解 C、当 时,方程有两个相等的实数解 D、当 时,方程总有两个不相等的实数解4. 抛物线 的顶点坐标是( )A、(1,2) B、(-1,2) C、 D、5. 若二次函数y=ax2+4x+a-1的最小值是2,则a的值为( )A、4 B、-1 C、3 D、4或-16. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).
3. 已知关于 的方程 ,下列说法正确的是( )A、当 时,方程无解 B、当 时,方程有一个实数解 C、当 时,方程有两个相等的实数解 D、当 时,方程总有两个不相等的实数解4. 抛物线 的顶点坐标是( )A、(1,2) B、(-1,2) C、 D、5. 若二次函数y=ax2+4x+a-1的最小值是2,则a的值为( )A、4 B、-1 C、3 D、4或-16. 如图, 是 的弦, 交 于点 ,点 是 上一点, ,则 的度数为( ).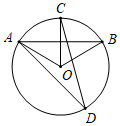 A、30° B、40° C、50° D、60°7. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到8. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )
A、30° B、40° C、50° D、60°7. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到8. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA=12,则阴影部分(即四边形AEOF)的面积是( )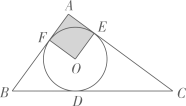 A、4 B、6.25 C、7.5 D、99. 已知点A ,B ,C 在二次函数y=-3x2+k的图象上,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、10. 如图,将 绕点C顺时针旋转得到 ,使点A的对应点D恰好落在边 上,点B的对应点为E,连接 .下列结论一定正确的是( )
A、4 B、6.25 C、7.5 D、99. 已知点A ,B ,C 在二次函数y=-3x2+k的图象上,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、10. 如图,将 绕点C顺时针旋转得到 ,使点A的对应点D恰好落在边 上,点B的对应点为E,连接 .下列结论一定正确的是( )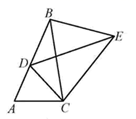 A、 B、 C、 D、11. 如图,⊙O的弦BC长为8,点A是⊙O上一动点,且∠BAC=45°,点D,E分别是BC,AB的中点,则DE长的最大值是( )
A、 B、 C、 D、11. 如图,⊙O的弦BC长为8,点A是⊙O上一动点,且∠BAC=45°,点D,E分别是BC,AB的中点,则DE长的最大值是( ) A、4 B、4 C、8 D、812. 二次函数 ( 是常数, )的自变量x与函数值y的部分对应值如下表:
A、4 B、4 C、8 D、812. 二次函数 ( 是常数, )的自变量x与函数值y的部分对应值如下表:…
0
1
2
…
…
…
且当 时,与其对应的函数值 .有下列结论:① ;②-2和3是关于x的方程 的两个根;③ .其中,正确结论的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
13. 若关于x的一元二次方程 有实数根,则m的取值范围是 .14. 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为.
 15. 已知△ABC的三条边长分别为6cm,8cm,10cm,则这个三角形的外接圆的面积为cm2 . (结果用含 的代数式表示)16. 有一个二次函数的图象,三位同学分别说了它的一些特点:
15. 已知△ABC的三条边长分别为6cm,8cm,10cm,则这个三角形的外接圆的面积为cm2 . (结果用含 的代数式表示)16. 有一个二次函数的图象,三位同学分别说了它的一些特点:甲:与 轴只有一个交点;
乙:对称轴是直线 ;
丙:与y轴的交点到原点的距离为3.
满足上述全部特点的二次函数的解析式为.
17. 有x支球队参加篮球比赛,每两队之间都比赛一场,共比赛了45场,则根据题意列出方程 .三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中,△ABC的顶点A在格点上,B是小正方形边的中点,经过点A , B的圆的圆心在边AC上.
 (1)、弦AB的长等于;(2)、请用无刻度的直尺,在如图所示的网格中,找出经过出点A , B的圆的圆心O , 并简要说明点O的位置是如何找到的(不要求证明) .19. 关于x的一元二次方程2x2﹣mx+n=0.(1)、当m﹣n=4时,请判断方程根的情况;(2)、若方程有两个相等的实数根,当n=2时,求此时方程的根.20. 已知二次函数y=﹣x2+bx+c , 函数值y与自变量x之间的部分对应值如下表:
(1)、弦AB的长等于;(2)、请用无刻度的直尺,在如图所示的网格中,找出经过出点A , B的圆的圆心O , 并简要说明点O的位置是如何找到的(不要求证明) .19. 关于x的一元二次方程2x2﹣mx+n=0.(1)、当m﹣n=4时,请判断方程根的情况;(2)、若方程有两个相等的实数根,当n=2时,求此时方程的根.20. 已知二次函数y=﹣x2+bx+c , 函数值y与自变量x之间的部分对应值如下表:x
…
﹣4
﹣1
0
1
…
y
…
﹣2
﹣1
﹣2
﹣7
…
(1)、此二次函数图象的对称轴是直线,此函数图象与x轴交点个数为 .(2)、求二次函数的函数表达式;(3)、当﹣5<x<﹣1时,请直接写出函数值y的取值范围.21. 如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m. (1)、求拱桥的半径;(2)、有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由;22. 已知PA , PB分别与⊙O相切于点A , B , ∠APB=76°,C为⊙O上一点.
(1)、求拱桥的半径;(2)、有一艘宽为5m的货船,船舱顶部为长方形,并高出水面3.4m,则此货船是否能顺利通过此圆弧形拱桥,并说明理由;22. 已知PA , PB分别与⊙O相切于点A , B , ∠APB=76°,C为⊙O上一点. (1)、如图①,求∠ACB的大小;(2)、如图②,AE为⊙O的直径,AE与BC相交于点D , 若AB=AD . 求∠EAC的大小.23. 如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
(1)、如图①,求∠ACB的大小;(2)、如图②,AE为⊙O的直径,AE与BC相交于点D , 若AB=AD . 求∠EAC的大小.23. 如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y. (1)、若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;(2)、在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?24. 如图,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG .
(1)、若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;(2)、在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?24. 如图,在矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG . (1)、如图1,若在旋转过程中,点E落在对角线AC上,AF , EF分别交DC于点M , N .
(1)、如图1,若在旋转过程中,点E落在对角线AC上,AF , EF分别交DC于点M , N .①求证:MA=MC;
②求MN的长;
(2)、如图2,在旋转过程中,若直线AE经过线段BG的中点P , 连接BE , GE , 求△BEG的面积25. 在平面直角坐标系xOy中,已知抛物线 (k为常数).(1)、若抛物线经过点(1,k2),求k的值;(2)、若抛物线经过点(2k,y1)和点(2,y2),且y1>y2 , 求k的取值范围;(3)、若将抛物线向右平移1个单位长度得到新抛物线,当1≤x≤2时,新抛物线对应的函数有最小值 ,求k的值.